Пусть целое

- фиксировано. Наша цель показать, что для полиномов

степени меньшей

, выполняется тождество:
![$$(\star)\qquad\qquad \sum_{I\subset [n]} (-1)^{|I|} S\big(\sum_{i\in I} a_i\big) = 0,$$ $$(\star)\qquad\qquad \sum_{I\subset [n]} (-1)^{|I|} S\big(\sum_{i\in I} a_i\big) = 0,$$](https://dxdy-02.korotkov.co.uk/f/1/0/e/10e7e323f883bb8b345f13d6ee75489182.png)
где
![$[n]:=\{1,2,\dots,n\}$ $[n]:=\{1,2,\dots,n\}$](https://dxdy-02.korotkov.co.uk/f/d/9/7/d97082f65395d53e51cb73fb45d0a0e682.png)
.
Достаточно доказать

для каждой степени

, где

, и произвольных
целых неотрицательных чисел

. Тогда на произвольные полиномы

степени меньшей

утверждение распространяется по линейности, а на произвольные действительные

в виду того, что

- полином.
Интерпретируя каждое

как мощность некоторого множества

, так что все эти множества попарно не пересекаются, мы получаем, что

-- это количество отображений

из множества
![$[d]$ $[d]$](https://dxdy-02.korotkov.co.uk/f/9/4/7/9472d5e94ffe268646e668123bf20ec282.png)
во множество

.
Для каждого
![$i\in [n]$ $i\in [n]$](https://dxdy-03.korotkov.co.uk/f/6/f/3/6f3a934f7a007d6f580938f00ada3e5b82.png)
определим

как свойство, что образ

не пересекается с

. Далее, для
![$I\subset [n]$ $I\subset [n]$](https://dxdy-01.korotkov.co.uk/f/c/7/8/c78771d6e9d04eda949f284c0952c87782.png)
определим

как количество отображений из
![$[d]$ $[d]$](https://dxdy-02.korotkov.co.uk/f/9/4/7/9472d5e94ffe268646e668123bf20ec282.png)
в

обладающих свойствами

для всех
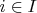
. Понятно, что

. Тогда согласно
формуле включений-исключений для свойств, выражение
![$$\sum_{I\subset [n]} (-1)^{|I|} S\big(\sum_{i\in I} a_i\big) = \sum_{I\subset [n]} (-1)^{|I|} N(\bar I) = \sum_{J\subset [n]} (-1)^{n-|J|} N(J)$$ $$\sum_{I\subset [n]} (-1)^{|I|} S\big(\sum_{i\in I} a_i\big) = \sum_{I\subset [n]} (-1)^{|I|} N(\bar I) = \sum_{J\subset [n]} (-1)^{n-|J|} N(J)$$](https://dxdy-01.korotkov.co.uk/f/4/1/5/415aefe1ec6d5a8ef820c1ac625c4c3782.png)
даёт умноженное на

количество функций не обладающих не одним из свойств (образ таких функций имеет непустое пересечение с каждым

). При

количество таких функций равно нулю, что доказывает тождество

.
P.S. Можно обобщить на произвольные целые

:
![$$\sum_{I\subset [n]} (-1)^{|I|} \left(\sum_{i\in I} a_i\right)^d = (-1)^n d!\ [x^d]\ \prod_{i=1}^n (e^{a_ix}-1).$$ $$\sum_{I\subset [n]} (-1)^{|I|} \left(\sum_{i\in I} a_i\right)^d = (-1)^n d!\ [x^d]\ \prod_{i=1}^n (e^{a_ix}-1).$$](https://dxdy-02.korotkov.co.uk/f/1/1/6/1165388b8d3f0c5004db489e40bbf44682.png)