Не очень понял тему, но попробовал решить (с помощью вычетов), и вот что получил.
Подскажите так или не так решать, думаю вообще ни чего не правильно.
Вычислить интеграл, если контур обходить против часовой стрелки.

Далее получаем точки:

т.к.

, то будет только одна точка

.
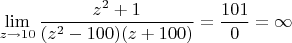
- полюс
![$$ \operatorname{Res}[f(z); 10]= \lim\limits_{z\to10}^{} \frac{z^ 2 +1}{(z-10)(z+10)(z+100)}(z-10) = \lim\limits_{z\to10}^{} \frac{z^ 2 +1}{(z+10)(z+100)} = \frac{101}{2200} $$ $$ \operatorname{Res}[f(z); 10]= \lim\limits_{z\to10}^{} \frac{z^ 2 +1}{(z-10)(z+10)(z+100)}(z-10) = \lim\limits_{z\to10}^{} \frac{z^ 2 +1}{(z+10)(z+100)} = \frac{101}{2200} $$](https://dxdy-02.korotkov.co.uk/f/9/a/b/9abb0a81b37647682dc6075b98d93f4682.png)
![$$ \operatorname{Res}= 2\pi i \sum\limits_{k=1}^{1} \operatorname{Res} [f(z); a_k] = 2\pi i \frac{101}{2200} = \frac{101 \pi i}{1100} $$ $$ \operatorname{Res}= 2\pi i \sum\limits_{k=1}^{1} \operatorname{Res} [f(z); a_k] = 2\pi i \frac{101}{2200} = \frac{101 \pi i}{1100} $$](https://dxdy-02.korotkov.co.uk/f/1/5/4/154eb3ae1ac8b0ffe456d32f609d860382.png)