Из http://dxdy.ru/topic10113-30.html

[toft]

Без интегрирования можно решить лишь приблизительно.
Сила сопротивления пропорциональна квадрату текущей скорости: F ~ $v^2$
В начале падения, когда влияние сопротивления ещё мало, скорость падения пропорциональна корню пройденного пути v ~ $x^{1/2}$
Таким образом, можно считать, что сила сопротивления, с точностью до поправок высших степеней, пропорциональна пути в первой степени: F ~ x
Тогда работу силы сопротивления воздуха при падении с высоты h приблизительно можно считать (по аналогии с работой, например, для сжатия пружины) равной $A = (F/2)h$, где F есть максимальное значение силы сопротивления воздуха $F = CpSv^2$
здесь v - искомая величина максимальной скорости (то есть скорость в момент падения штуки поперечным сечением S, у нас оно 1 кв м)
C - коэффициент сопротивления воздуху, берём 1.1 из справочника
p - плотность среды, то есть сухого воздуха при 20 град цельсия - 1.2 кг на м куб
Тогда уравнение сохранения энергии можно расписать так:
$mgh = mv^2/2 + CpSv^2/2$
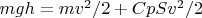
здесь m - масса штуки в 250 кг
g - ускорение свободного падения 10 м в сек за секунду
h - пройденный путь, сиречь высота падения - 20 метров
прочие величины даны выше.
Решая уравнение относительно v^2 получаем
$v^2 = 2mgh/(m + CpSh)$
Как видно, без учёта сопротивления воздуха (С=0), формула переходит в решение для свободного падения тела:
$v^2 = 2gh$
Подставляя численные значения, получим
$v^2 = 362$ (м в сек) в квадрате или
v = 19 м в сек
Без учёта сопротивления воздуха, эта величина равнялась бы 20 м в сек.

Очевидно, что такой жульский упрощённый способ учёта сопротивления среды имеет свои границы применения. Он явно не годится для учёта сопротивления воздуха при больших скоростях (высотах), ибо тогда допущение о том, что скорость растёт пропорционально корню из пройденного пути решительно уже не работает.
Для точного решения, справедливого во всём диапазоне высот и скоростей, необходимо решить дифуру, приведённую выше (хотя и это описание будет неточным, но вполне годным для высот до полу-километра, где плотность воздуха можно приблизительно считать постоянной. Но это уже дебри, далеко выходящие за рамки условия конкретной задачи).
Возможно, гадкий препод, озадачивший десятиклассников этой задачей, имел в виду ожидаемое решение примерно в вышеизложенном виде. Лично мне оно не очень нравится, но ничего лучшего я не придумал.
Впрочем, в любом случае, решение "прокисло" - ибо парнишка давно уже покончил и с колледжом, и с физикой, и с преподом.

[Mihr]

toft, сила сопротивления среды приблизительно пропорциональна квадрату скорости при больших значениях скорости тела относительно вязкой среды. При малых скоростях зависимость силы сопротивления среды от скорости движения тела в этой среде близка к линейной. Поэтому утверждение

toft в сообщении #1138449 писал(а):

Таким образом, можно считать, что сила сопротивления, с точностью до поправок высших степеней, пропорциональна пути в первой степени: F ~ x

едва ли можно считать верным.

[Pphantom]

Тема перемещена из форума «Физика» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.