Вроде бы, получилось...
(Оффтоп)
Лемма: для любого натурального

, дающего остаток 0,1,4 или 7 при делении на 9, найдётся натуральное число

такое, что

.
Доказательство: разделим

на 9 с остатком, пусть

. Тогда возможны 4 случая:
1)

. Тогда подходит

.
2)

. Тогда подходит

.
3)

. Тогда подходит

.
4)

. Тогда подходит

.
Теперь пусть

- взаимно простое с 10 натуральное число число. Тогда

.
1) Если мы подставим
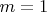
, то получим

, значит, в силу леммы

принимает все натуральные значения, дающие остатки 1,2,5,8 при делении на 9(кроме 1).
2) Если мы подставим

, то

, и получим

, значит, в силу леммы

принимает все натуральные значения, дающие остатки 2,3,6,0 при делении на 9.
3) Если мы подставим

, то

, и получим

, значит, в силу леммы

принимает все натуральные значения, дающие остатки 3,4,7,1 при делении на 9.
Таким образом, задача решена.