Добрый день.
Есть следующая задача:
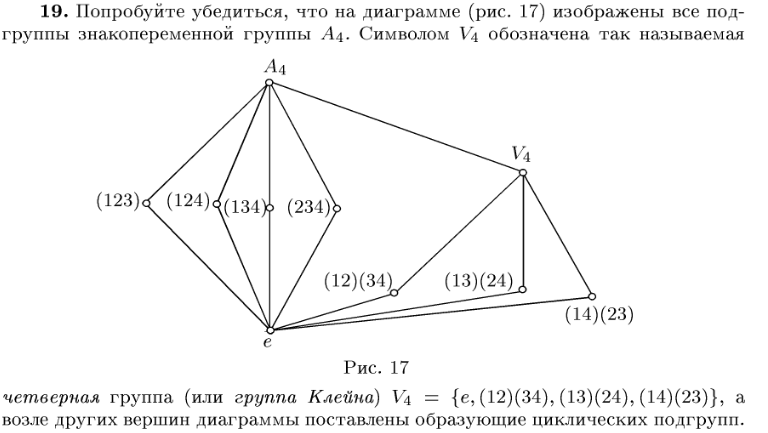
Я выписал все четные перестановки и очевидные циклические группы:
1) Единичная перестановка -

2) Трехэлементные перестановки (в соответствующих группах):




3) Четырехэлементные перестановки:



Однако по условию задачи необходимо убедиться что нет никаких других групп, кроме изображенных на диаграмме.
Наверное можно это сделать полным переобором всевозможных сочетаний перестановок, в процессе которого найдется и группа Клейна.
Но не хотелось бы таким заниматься. Подскажите, можно ли какими-то рассуждениями сократить перебор, или вообще обойтись без него?