QR-Разложение (II). Нахождение собственных векторов.

[Amateur_3D]

Тема QR - алгоритма уже обсуждалась здесь http://dxdy.ru/topic78209.html, но боюсь что за давностью лет мой вопрос никто не увидит.

Объясните пожалуйста такой ход в QR алгоритме (этот текст отсюда http://old.math.tsu.ru/EEResources/cm/text/6_2_4.htm):

"Если требуется определить не только собственные значения матрицы $A$, но и её собственные векторы, то в процессе построения последовательности матриц $A_{k}$ следует запоминать ортогональные матрицы
$P_{k}=Q_{1}\cdot ....\cdot Q_{k}$, вычисляемые по рекуррентной формуле:$P_{k+1}=P_{k}\cdot Q_{k+1}$"

Я раскладываю матрицу размерностью 10x10 метод Грэма-Шмидта (хотя какая разница). Собственные числа я получил.
Чтобы не решать систему из 10-ти линейных уравнений, как выше описанный приём реализовать "на лету".

Как я понял из текста, я собираю найденные на каждой итерации значения $Q_k$ и потом на следующей иттерации умножаю их на найденные в следующей (т.е. $Q_k \cdot Q_{k+1}$) и т.д.

Дело в том, что в итоге я получаю матрицу $P_{k}$ (как в тексте выше), со значениями лишь на главной диагонали.

MatLab (да и онлайн-сервисы) дают совсем другие результаты.

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);

Cм. выше.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Lia]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»

[svv]

Последовательность матриц $A_k$ к чему у Вас стремится? Обозначим эту матрицу $A_{\infty}$, а предел $P_k$ — $P_{\infty}$ (можете предложить свои обозначения). Судя по тексту, у вас равенство $A=P_{\infty}A_{\infty}P_{\infty}^T$ не выполняется (хотя обязано, так как $A_{\infty}=P_{\infty}^T A P_{\infty}$). Проверьте, пожалуйста, выполнение этих равенств.

[Amateur_3D]

svv, равенство $A = P_{\infty} \cdot A_{\infty} \cdot P_{\infty}^T$ у меня выполняется. Ту формулу, что вы написали даёт собственные числа на главной диагонали матрицы $A$ за N-ое количество итераций

Цитата:

Собственные числа я получил .

(цитирую сам себя).

Вопрос задам снова: Как получить собственные векторы в QR - алгоритме "на лету", т.е. считая параллельно собственные значения.

Может кто-нибудь этот момент объяснить, расписать ?

Задам может быть глупый вопрос: Как эти "$Q$" перемножать ?

Немного позднее, если тема не "уедет" вниз, придётся привести простенький пример моих "УСИЛИЙ"

[svv]

Amateur_3D в сообщении #1109977 писал(а):

Как получить собственные векторы в QR - алгоритме "на лету", т.е. считая параллельно собственные значения.

Не знаю.

Более того.

Amateur_3D в сообщении #1109597 писал(а):

"Если требуется определить не только собственные значения матрицы $A$, но и её собственные векторы, то в процессе построения последовательности матриц $A_{k}$ следует запоминать ортогональные матрицы
$P_{k}=Q_{1}\cdot ....\cdot Q_{k}$, вычисляемые по рекуррентной формуле:$P_{k+1}=P_{k}\cdot Q_{k+1}$"

Похоже, здесь подразумевается, что матрица $P_\infty$ при завершении итерационного процесса будет всегда содержать собственные векторы.

Это справедливо в случае, если $A$ — нормальная матрица ($AA^*=A^*A$). В частности, если $A$ симметрична. В этом случае $A_\infty$ должна быть диагональной матрицей, и легко видеть, что тогда $P_\infty$ действительно состоит из собственных векторов.

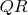
С другой стороны, это неверно в общем случае. Возьмём в качестве исходной $A$ правую треугольную матрицу. Тогда $QR$-алгоритму «нечего делать»: разложение $A=EAE$ является искомым. Но столбцы $E$ вовсе не являются собственными векторами.

[Amateur_3D]

Всё Я разобрался. Ошибка банальная: перемножал скалярно, а надо матрица на матрицу.

svv, Вы пишите ерунду. Много "умной воды". Не знаете - не отвечайте.

Спасибо всем, кто прочёл !

Тема ЗАКРЫТА.

[svv]

Ну, почему же ерунду? У Вас не получались собственные векторы. В материальчике, которым Вы руководствовались, написано: «Пусть $A$ – произвольная вещественная матрица», а для вычисления собственных векторов без всяких оговорок предлагается вычислять произведение преобразующих матриц $Q_1...Q_k$, как Вы и поступали. Но в общем случае это произведение не даёт собственные векторы, только в специальном. Вы с этим не согласны?