электростатика, конденсаторы

[ULTROZY]

Здравствуйте.
Даны 4 металлические пластины площадью $S$ параллельные и каждый находящийся на расстоянии $d$ друг от друга. Их подключили к источникам с напряжениями $4U$ и $5U$ (см. рис.):

Найти заряд на внешних пластинах.
Моё решение

Электростатическое поле напряжённостью $E_1$ действует на 3 пластину (зарядом $q_2$), поэтому её собственная напряжённость равна $E_1\prime=E_1=\frac{2U}{d}$. Также она равна $E_1\prime=\frac{q_2_1}{2\varepsilon_0 S}+\frac{q_2_2}{2\varepsilon_0 S}=\frac{q_2}{2\varepsilon_0 S}$. Отсюда получаем $q_2=\frac{4\varepsilon_0 US}{d}$. Аналогично со 2 пластинкой зарядом $-q_1$: $E_2\prime=E_2=\frac{2,5U}{d}$; $E_2\prime=\frac{-q_1_1}{2\varepsilon_0 S}+\frac{-q_1_2}{2\varepsilon_0 S}=\frac{q_1}{2\varepsilon_0 S}$ $\Rightarrow$ $q_1=\frac{5\varepsilon_0 US}{d}$
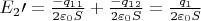
Тогда на внешних обкладках системы заряды: $q_1=\frac{5\varepsilon_0 US}{d}$ и $-q_2=-\frac{4\varepsilon_0 US}{d}$

[profrotter]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Карантин»
Причина переноса:
Отсутствуют собственные попытки решения задачи.

(Подробно)

Forum Administration в сообщении #27356 писал(а):

I. Нарушения и санкции
1) Нарушением считается:
г) Поиск халявы в отношении учебных задач и вопросов; публикация полных готовых решений учебных задач (см. п. III-2); вынесение на обсуждение задач еще не прошедших он-лайн и заочных олимпиад.

Приведите собственные содержательные попытки решения задачи и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума

[profrotter]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (Ф)»
Причина переноса: вернул.

[svv]

ULTROZY в сообщении #1108177 писал(а):

Электростатическое поле напряжённостью $E_1$ действует на 3 пластину (зарядом $q_2$), поэтому её собственная напряжённость равна $E_1\prime=E_1=\frac{2U}{d}$.

Эта фраза совсем непонятна.

У меня получились другие числа. Я решал так. Из того, что 1) поле одной пластины симметрично относительно её плоскости, 2) суммарный заряд всех пластин равен нулю и 3) выполняется принцип суперпозиции, следует, что вне конденсатора поле нулевое. Из теоремы Гаусса следует, что скачок (разность значений справа и слева) электрического поля на любой пластине $E_x(x^{+})-E_x(x^{-})=\frac{q}{\varepsilon_0 S}$, где $q$ — её заряд. Отсюда по зарядам пластин (верхняя строка) находим поля в промежутках между пластинами (средняя строка) и затем потенциалы пластин (нижняя строка):
$\begin{matrix}q:&-q_2&&-q_1&&+q_2&&+q_1\\E:&&-\frac{q_2}{Cd}&& -\frac{q_1+q_2}{Cd}&&-\frac{q_1}{Cd}&\\\varphi:&0&&\frac{q_2}{C}&&\frac{q_1+2q_2}{C}&&\frac{2q_1+2q_2}{C}\end{matrix}$
Здесь обозначено $C=\varepsilon_0 S/d$. Получаем систему
$\begin{bmatrix}2&1\\1&2\end{bmatrix}\begin{bmatrix}q_1\\q_2\end{bmatrix}=\begin{bmatrix}CU_1\\CU_2\end{bmatrix}$