Sirion, спасибо! Правда, картинка проблемой не была. Я позавчера ещё (для себя

) нарисовал вот такую:

Попробовал

и, как и Вы, остановился на 24-угольнике. Поясню смысл обозначений.
Цвета. Сразу видно, что при любом

диагонали разбиваются на три серии.
Стрелки. У каждой диагонали есть 1-конец и 2-конец, исходя из коэффициента при номере вершины в сумме

. 1-конец помечен стрелкой, 2-конец не помечен.
Номера. Будучи прямо связаны с Вашими, здесь они уже имеют более «продвинутый» смысл. Пусть номер диагонали — это число у её 2-конца, на картинке оно имеет тот же цвет, что сама диагональ. Тогда в каждой точке пересечения диагоналей сумма трёх их номеров равна нулю.
Звёздочки. Все диагонали можно получить таким способом. Один человечек идёт против часовой стрелки, становясь на каждом шаге на соседнюю вершину. Другой бежит по часовой стрелке с двойной скоростью, т.е. прыгает через одну. На каждом шаге они перебрасывают между собой отрезок. Если человечки стартуют из одной вершины (
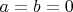
), то в трёх вершинах у них будут места встречи, они и обозначены звёздочками.
Картинка (не обязательно моя или Ваша, а «вообще») изумительно красивая.