Лицевая сторона:
Противоположные последовательности чисел: 1, 2, 3, 4, 5,…; -1,-2,-3,-4,-5,...
Выразим формулами:

(n - номер взятого члена, при отрицательном или положительном значении n. Выражения

следует понимать: вычитание от номера взятого члена).
Пример:

При

имеем:

1)

2)

3)

4)

При

имеем:

1)

2)

3)

Пример:

При

имеем:

1)

2)

3)

4)

При

имеем:

1)

2)

3)
 Трехгранная:
Трехгранная: 
Противоположные последовательности чисел: 1, 3, 6, 10, 15,…; -1,-3,-6,-10,-15,...
Выразим формулами:

.,

.,

Пример:

При

имеем:

1)

2)

3)

4)

5)

6)

7)

8)

9)

При

имеем:

1)

2)

3)
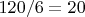
4)

5)

6)

7)

Пример:

При

имеем:

1)

2)

3)

4)

При

имеем:

1)

2)

3)
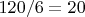
Пример:

При

имеем:

1)

2)

3)

4)

5)

6)

7)

8)

9)
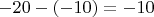
При

имеем:

1)

2)

3)
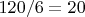
4)

5)

6)

7)
 Четырехгранная:
Четырехгранная:
Противоположные последовательности чисел: 1, 4, 9, 16, 25.....; -1,-4,-9,-16,-25.....
Выразим формулами:

.,

.
Пример:

При

имеем:

1)

2)

3)

4)
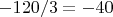
5)

6)

7)

8)

9)

При

имеем:
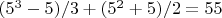
1)

2)

3)

4)

5)

6)

7)

Пример:

При

имеем:

1)

2)

3)

4)

5)

6)

7)

8)

9)

При

имеем:

1)

2)

3)

4)

5)

6)

7)
