Два бруска массами
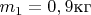
и

, лежащие на гладком полу, соединены невесомой пружиной.
Бруски удерживают так, что пружина сжата на

. Сначала отпускают первый брусок, а в тот момент, когда пружина не деформирована, отпускают и второй. Найдите максимальную деформацию (в см) пружины в процессе дальнейшего движения.
Единственное, в чем мне удалось продвинуться – нахождение скорости первого бруска, когда отпускают второй.
1)Обозначим жёсткость пружины как

, начальная деформация как

2)скорость первого бруска в момент когда отпускают второй, обозначим ее


, отсюда

Подскажите, что делать дальше?