MihrНе в упрёк Вам, а только ради сути дела приведу известное сравнение (сказанное, правда, кем-то по другому поводу, но здесь оно тоже подходит, хотя и звучит грубо): методические преимущества концепции "орбит" сродни преимуществам воровства перед честным трудом. :)
Рассказывая ученикам о таких сложных вещах, как квантовая теория атома, преподаватель вынужден сделать выбор между двумя путями:
Первый путь:
перечислить основные факты, необходимые в дальнейшем для выстраивания ещё и множества других фактов в единую картину. В нашем примере к основным фактам относится только формула (17.5) из цитированного Вами текста Савельева, нужная в дальнейшем для обсуждения квантовых переходов с поглощением и испусканием фотонов, и формула (17.4), причём последняя в квантовой механике не имеет смысла радиуса "орбиты", а служит оценкой "радиуса" сферически симметричного (шарообразного, но без чёткой поверхности) "облака вероятности" или, говоря чуть иначе, "орбитали".
Постоянная Ридберга, т.е. множитель с размерностью энергии в (17.5), а также радиус Бора (17.4) - всё это с точностью до безразмерных множителей элементарно выводится из соображений размерности через заданные фундаментальные константы



Полный же вывод формулы для квантованных уровней энергии (и для момента импульса) очень сложен: он даётся анализом уравнения Шрёдингера, его студенты изучают обычно лишь на 3-ем курсе, уже освоив дифф. уравнения. Этот факт школьники тоже должны знать, ведь это суровая и важная правда жизни: есть физика, требующая от учёного гораздо большей подготовки, чем получает школьник на уроках физики в школе!
Второй путь:
предъявить школьнику лишь фокус-покус - это цитированный выше текст из Савельева - посредством которого якобы элементарно выводится квантование уровней энергии. (Да, подобный фокус-покус придумал Бор, но это было во времена ещё только первых интуитивных поисков правдоподобной теории; через примерно 13 лет выяснилось, что идея об орбитах - ошибка, а формула для

всё-таки с хорошей точностью верна для атома водорода, хотя "главное квантовое число" имеет вовсе не тот смысл, о котором речь в (17.1). Поэтому сегодня об "орбитах Бора" можно говорить только в плане обзора истории физики, но никак не в качестве практически применимой "элементарной модели атома". Причём, историю физики лучше рассказывать не школьникам, а людям, которые уже более-менее знают современную квантовую физику).
Хотя считается, что к одному из методических преимуществ "орбит" относится лёгкость, с которой школьники усваивают такой вывод, я нахожу этот аргумент очень зыбким; ведь следуя подобной логике можно вообще вместо физики начать рассказывать сказки - они же легче усваиваются, чем сложные уравнения. Напомню теперь попросту
неверные "результаты" модели, изложенной в цитированном выше тексте Савельева.
В квантовой механике нет формул (17.1)--(17.3). Квантованные значения момента импульса

вовсе не так связаны с главным квантовым числом

как утверждается в (17.1). И кроме того, картинка "орбит" с сохраняющимся моментом импульса ведёт школьника к ошибочнуму представлению об атоме как о чём-то плоском (расположенном в плоскости орбиты). Такая картинка находится в явном противоречии с использумыми в химии и далее в физике молекул и в физике твёрдых тел представлениями об атомах как о "шарах". Разве может иметь методическую ценность ошибочный (хотя и сказочно лёгкий) вывод, порождающий противоречия с остальными областями физики?
Правильная картина, следующая из уравнения Шредингера, вот какая: орбитальная часть

волновой функции электрона в атоме зависит от трёх квантовых чисел



(т.е. имеется

значений числа

при каждом

это общий результат квантовой теории момента имульса.)
В квантовой механике (не в модели Бора!) выводится, что в атоме водорода уровни энергии зависят только от

- вот это выражение и называется главным квантовым числом

и вот именно оно входит в формулу (17.5). Отсюда видно, например, что в состоянии с самым нижним уровнем энергии (т.е. при

) момент импульса равен нулю,

и его проекция на любую ось тоже равна нулю:

Т.е. формула (17.1) просто врёт!
Учитывая указанные выше значения квантовых чисел,
легко подсчитать, что уровню энергии с заданным

принадлежат

различных волновых функций

Если учесть ещё и допустимые значения спинового квантового числа, а их всего два, то получается, что на каждом уровне энергии

имеется

квантовых состояний электрона.
Для атомов, более сложных, чем атом водорода, квантовая механика позволяет находить уровни энергии атома лишь численными приближёнными методами, простой общей формулы уже нет. Оказывается, что уровни энергии

электрона (если их приближённо определить) в атоме с ядром, экранированным другими электронами, т.е. при некулоновском потенциале, зависят от квантовых числ
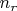
и

уже порознь, но значения энергии с разными
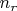
и

при заданном

получаются близкими; а с разными значениями

уровни энергии разнятся сильно. Поэтому "главное квантовое число" и в случае сложных атомов оказывается полезным для классификации уровней на шкале энергии. Этот факт вместе с принципом заперта Паули ведёт к известной в химии картине последовательного заполнения одноэлектронных квантовых состояний в атоме электронами - к "периодической системе элементов".
Короче говоря, в квантовой физике нет (хотя
в истории физики были) отдельной модели "орбит Бора" в атоме водорода и модели "орбиталей" в химии или в физике твёрдых тел, а есть единая, логичная, качественно и количественно удовлетворительная квантовая картина атомов, основанная на понятии волновой функции электрона

Имхо, школьникам лучше рассказывать доступную их пониманию часть такой правды (с указаниями на полные курсы квантовой теории, которые ребята смогут изучить в процессе своего дальнейшего образования, уже внешкольного), чем закладывать в их головы простую, но неверную картинку "орбит" ради простоты неверного же вывода одной правильной формулы для
