Скажем, кидаем его шесть раз подряд.
1) Какова вероятность выпадения единицы все шесть раз?
2) Какова вероятность того, что выпадут все шесть граней?
3) Если в этой серии такое случилось, то какова вероятность того, что в первый раз выпала тройка?
Ну и тому подобное. Когда наступит полное понимание, можно сделать нестандартный кубик с разными вероятностями. А уж потом перенести это дело в туалет или в космос.
И ведь слышал я ровно эти слова на семинаре. Блажен тот, кто начинает интересоваться ТВ в школе. В универе не успеваешь оглянуться, а уже ЦПТ
 Cash
Cash, а мне другая цитата вспомнилась: "
Не уж то был — гадюка злая."

1)

2)

3) Пусть

- в этой серии такое случилось.

- в первый раз выпала тройка.

-вероятность того, что в первый раз выпала тройка, при условии того, что все шесть раз выпали разные числа.
Ну так, если выполняется гипотеза

, то мы просто распределяем различные грани между бросками, что есть просто перестановки.
По факту получается, что число перестановок всех граней

, если зарезервировать первое место за тройкой, то таких перестановок с тройкой на первом месте будет
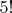
. Потому вероятность

.
Ну или просто мы выбираем наугад место для тройки. 1 благоприятный исход из шести, потому

.
Верно?
-- 08.01.2016, 13:34 --Вроде как тогда и в задаче про туалеты в первом пункте будет

по тем же причинам, потому как

не при делах, для них просто места выбираются. Правильно?