Что есть электрический потенциал?

[мат-ламер]

В связи с интересной дискуссией, развернувшейся в теме http://dxdy.ru/topic104069.html, хочу задать два вопроса по сущности электрического потенциала. Я понял, что мои понятия об оном не совпадают с понятием о потенциале, которые имеют участники той дискуссии. Обратившись к учебнику (Сивухин), я чёткости не нашёл, поэтому решил обратиться за помощью к форуму. 1) Потенциал электрического поля в данной точке я всегда представлял, как работу, которую необходимо затратить на перемещение единичного положительного заряда из данной точки в точку, потенциал которой принят за нулевой (часто, но не всегда, это условно бесконечная точка). (См., например, Детлаф и Яворский, т.2., пар.3.2, стр. 35 (посередине)). Судя по следующей цитате

Munin в сообщении #1085192 писал(а):

Замечая, что $A_1=\varphi_\mathrm{far},\quad A_3=-\varphi_\mathrm{near}$

Munin представляет себе потенциал как работу по перемещению заряда из точки с нулевым потенциалом в данную. Чёткости в данном вопросе у Сивухина нет. Однако моё понимание совпадает с пониманием потенциала, как скалярного поля, градиент которого с обратным знаком порождает электрическое поле. В частности, потенциал точки вблизи положительного заряда отрицательный. 2) Я понимаю, что определение потенциала через работу главное. В то время, как определение через градиент может содержать некоторые нюансы. Там надо предполагать, что пробный заряд не вызывает перераспределение зарядов исходного поля. Рассмотрим простой пример. Возьмём металический шар конечных размеров незаряженный. Сам по себе он поля не создаст. Если определять потенциал через градиент, то и потенциал этого поля будет нулевой. Однако, если пробный заряд разместить вблизи шара, то он будет притягиваться им. Значит на самом деле потенциал металического шара ненулевой. (Второй вопрос задан с целью осмыслить сообщение от Amonа в http://dxdy.ru/post1085254.html#p1085254).

[DimaM]

мат-ламер в сообщении #1085322 писал(а):

Однако моё понимание совпадает с пониманием потенциала, как скалярного поля, градиент которого с обратным знаком порождает электрическое поле. В частности, потенциал точки вблизи положительного заряда отрицательный.

Традиционно принято наоборот.

мат-ламер в сообщении #1085322 писал(а):

Рассмотрим простой пример. Возьмём металический шар конечных размеров незаряженный. Сам по себе он поля не создаст. Если определять потенциал через градиент, то и потенциал этого поля будет нулевой. Однако, если пробный заряд разместить вблизи шара, то он будет притягиваться им. Значит на самом деле потенциал металического шара ненулевой.

Странный несколько пример. Если у нас есть только незаряженный металлический шар, то потенциал вблизи него нулевой. А если мы еще добавим точечный заряд, то потенциал станет ненулевым (в какой-то точке, впрочем, останется нулевым). Ну так это две разные системы зарядов, чего тут удивительного.

[мат-ламер]

DimaM в сообщении #1085324 писал(а):

мат-ламер в сообщении #1085322 писал(а):

Однако моё понимание совпадает с пониманием потенциала, как скалярного поля, градиент которого с обратным знаком порождает электрическое поле. В частности, потенциал точки вблизи положительного заряда отрицательный.

Традиционно принято наоборот.

Я ориентировался на Сивухина (формула 18.5 из параграфа 18). Он пишет, что $\mathbf{E}=-\operatorname{grad} \varphi$. В частности, если поле $\mathbf{E} = q \mathbf{r}||r||^{-3}$, то его потенциал $\varphi = -q||r||^{-1}$. (Это уже моё) (Может не так градиент взял?).

[DimaM]

мат-ламер в сообщении #1085329 писал(а):

Он пишет, что $\mathbf{E}=-\operatorname{grad} \varphi$.

Правильно пишет.

мат-ламер в сообщении #1085329 писал(а):

В частности, если поле $\mathbf{E} = q \mathbf{r}||r||^{-3}$, то его потенциал $\varphi = -q||r||^{-1}$. (Это уже моё) (Может не так градиент взял?).

Именно что не так.
Еще и значки странные у вас: нормально писать ${\bf E}=\dfrac{q{\bf r}}{r^3},\; \varphi=\dfrac{q}{r}$.

[rustot]

мат-ламер в сообщении #1085329 писал(а):

Он пишет, что $\mathbf{E}=-\operatorname{grad} \varphi$

Вектор $\nabla \varphi$ направлен в ту сторону, в которую $\varphi$ прирастает наиболее быстро. То есть при движении вдоль $\vec{E}$ потенциал убывает

мат-ламер в сообщении #1085329 писал(а):

Может не так градиент взял?

$E_x = -\frac{\partial}{\partial x} \varphi = - q \frac{\partial}{\partial x} \frac{1}{r} = q \frac{x}{r^3}$

[Munin]

Насчёт значков: в математике принято обозначать вектор каким-нибудь символом, а его норму - дополнительным значком. Например: $\mathbf{r},\|\mathbf{r}\|,$ или $x,\|x\|.$

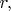
В физике принято немного иначе, чтобы не загромождать запись: вектор и его модуль (норму по скалярному произведению) обозначают одной и той же буквой разными шрифтами. Например: $\mathbf{r},r,$ или $\vec{r},r.$ Кроме того, для радиус-вектора повсеместно используется только буква $r,$ хотя в математике частенько встречается $x$ - в физике это встречается только в индексной записи $x^i=(x^1,x^2,\ldots,x^n).$

Так что: $\mathbf{E}=q\mathbf{r}\,r^{-3},\quad\varphi=q\,r^{-1}$ - это читаемо. А вставлять в одну формулу $\mathbf{r}$ и $||r||$ - это перебор.

мат-ламер в сообщении #1085322 писал(а):

Я понимаю, что определение потенциала через работу главное. В то время, как определение через градиент может содержать некоторые нюансы. Там надо предполагать, что пробный заряд не вызывает перераспределение зарядов исходного поля.

Насчёт определения: как раз наоборот. Именно определение через работу содержит этот нюанс. А определение через градиент - нет.

Именно в этом нюансе возникает проблема в задачах с проводниками. Проводники дают "изображения (отражения)" окружающих зарядов, в том числе и пробного. Если внешние заряды перемещаются, то перемещаются и заряды по поверхности проводников, то есть, меняются и изображения. То есть, определение через работу, буквально понятое, становится неверным. Необходимо проделать дополнительный шаг:
1. Зафиксировать все заряды, кроме пробного. Это означает, (мысленно) заменить проводники на диэлектрики, и воспроизвести на них те распределения зарядов, которые были созданы перед этим на проводниках.
2. Только после этого вносить пробный заряд, и измерять с его помощью все потенциалы по определению через работу.

Шаг 1 можно заменить рассуждением:
1'. Допустим, что пробный заряд взят достаточно малым, чтобы никак не повлиять на распределение всех остальных зарядов (точнее, повлиять пренебрежимо мало).
Но это не всегда возможно. Например, в квантовых задачах нельзя взять заряд меньше заряда электрона $e,$ а это может оказаться не малой, а существенной величиной, например, в атоме.

В рассматриваемой задаче эта же трудность, как указал amon (а я, к стыду своему, упустил из виду): пробный заряд должен быть достаточно малым, чтобы с его помощью можно было измерить потенциал через работу; но в то же время пробный заряд не должен быть малым, потому что его появление должно создать разницу между энергиями двух систем проводников.

[amon]

мат-ламер в сообщении #1085322 писал(а):

Я понимаю, что определение потенциала через работу главное.

Мы с Вами взрослые люди, и во избежании всяких неприятностей должны четко представлять, откуда берутся дети потенциалы. Никаких потенциалов в природе нет. Их теоретики придумали, что бы уравнения Максвелла решать. В стационарном случае в электростатике исходным является уравнение $\mathbf{E}=-\nabla\varphi-\frac{1}{c}\frac{\partial\mathbf{A}}{\partial t}.$ Если в этом уравнении положить $\mathbf{A}=0$ и сказать, что $\varphi(\infty)=0,$ то окажется, что для неподвижных зарядов $\varphi$ совпадет с наблюдаемой - работой по перемещению зарядов. Последнее наблюдение и используется как определение в школьных учебниках, что бы не рвать детям мозг калибровочными преобразованиями. Можно поступить по-другому: положить $\varphi=0,$ и тогда (процитирую себя, любимого) "во всей вселенной все потенциалы сразу зануляются, все вольтметры превращаются в тыквы, а эталон вольта становится эталоном нуля". Такая калибровка иногда удобнее стандартной, но прямого физ. смысла величина $\mathbf{A}$ не имеет. Можно, в принципе, выбрать что-то промежуточное, правда, непонятно зачем. Это я к тому, что определение потенциала через работу - очень частный случай, выполняющийся не при всех условиях.

[peripatetik]

мат-ламер в сообщении #1085322 писал(а):

Потенциал электрического поля в данной точке я всегда представлял, как работу, которую необходимо затратить на перемещение единичного положительного заряда из данной точки в точку, потенциал которой принят за нулевой...

НЕ единичного, а бесконечно малого (пробного), в том-то и суть. (Если заряд конечный, то сдвигая его Вы меняете распределения остальных зарядов.) Он потому и называется пробный, так как он только "пробует" систему, не меняя ее.

[arseniiv]

Пробного и единичного. Если брать в разных случаях пробные разной величины, получится катавасия.

-- Чт дек 24, 2015 17:21:38 --

А бесконечная малость не нужна (физика не манипулирует в описаниях экспериментов бесконечно точными величинами, ага) и невозможна вообще. И выше об этом писали.

[peripatetik]

arseniiv в сообщении #1085440 писал(а):

Пробного и единичного. Если брать в разных случаях пробные разной величины, получится катавасия.

Нет, бесконечно малого, но работу надо не забыть поделить на величину пробного заряда.

[Munin]

Добавлю, что в электростатике выполняется $[\nabla\mathbf{E}]=0,$ а в нестационарном случае это вообще говоря не выполняется. Именно это условие позволяет ввести такую функцию $\varphi,$ что $\mathbf{E}=-\nabla\varphi$ (минус чисто по физической традиции, в математике его не пишут). Кроме того, необходимо топологическое условие: чтобы рассматриваемые функции были заданы во всём пространстве, или по крайней мере в односвязной области (каждая петля может быть стянута в точку).

В нестационарном случае такую функцию ввести нельзя (по той причине, что $[\nabla\mathbf{E}]\ne 0$), и в формулу приходится добавлять второе слагаемое. Но на самом деле, ситуация аналогична, просто в 4-мерном пространстве-времени:
- мы имеем вместо векторного электрического поля 6-компонентную величину: антисимметричный тензор 2 ранга - тензор электромагнитного поля $F_{\mu\nu}$;
- для этой величины выполняется аналогичное уравнение $\partial_{[\lambda}F_{\mu\nu]}=0$;
- и благодаря ему, возможно ввести такую функцию $A_\mu,$ что $F_{\mu\nu}=\partial_{[\mu}A_{\nu]}.$
Именно 3-мерные проекции этих 4-мерных величин и будут электрическим полем и потенциалом (причём добавляется ещё и магнитное поле, и потенциал $\mathbf{A}$ оказывается тесно связанным с ним: $\mathbf{B}=[\nabla\mathbf{A}]$).
Кроме того, добавляется и топологическое условие, несколько более сложное: 2-связность, то есть, что каждая 2-мерная оболочка может быть стянута в точку (в 4-мерном пространстве эта оболочка является в то же время аналогом петли). Это условие также порождает вышеупомянутое условие при 3-мерной проекции. А для магнитного поля оно имеет другую проекцию: для существования вектор-потенциала заданного магнитостатического поля нужна опять-таки 2-связность области пространства (иначе можно задать "магнитный монополь" - "магнит с одним полюсом", для которого вектор-потенциала не будет).

-- 24.12.2015 15:38:21 --

arseniiv
peripatetik
Вы оба правы и оба неправы в разных нюансах, дополняя друг друга :-)
arseniiv: прав в том, что "бесконечной малости" в физике не бывает, бывает "пренебрежимая малость".
peripatetik: прав в том, что заряд не должен быть единичным, но на его величину попросту надо поделить.

[amon]

Munin в сообщении #1085445 писал(а):

В нестационарном случае такую функцию ввести нельзя

Это-то обычно знают, а вот то, что в электростатике можно использовать калибровку $\varphi=0$ для некоторых является откровением.

[Munin]

amon в сообщении #1085448 писал(а):

Это-то обычно знают, а вот то, что в электростатике можно использовать калибровку $\varphi=0$ для некоторых является откровением.

Можно-то можно, но это просто некрасиво:
- потенциал $\mathbf{A}$ оказывается зависим от времени: $\mathbf{A}=\mathbf{a}t$ (линейность обязательна, поскольку $\mathbf{E}$ стационарно);
- и отсюда автоматически $\mathbf{E}=-\mathbf{a}/c,$ то есть вместо красивой теоремы векторного анализа получается банальность.

($+\mathbf{C}(\mathbf{r})$ не пишу.)

-- 24.12.2015 15:47:32 --

Впрочем, в некоторых задачах электродинамики (не электростатики) эта калибровка оказывается полезной.

-- 24.12.2015 15:52:22 --

Munin в сообщении #1085445 писал(а):

$F_{\mu\nu}=\partial_{[\mu}A_{\nu]}$

Точнее, физики, опять же по традиции, используют такую формулу: $F_{\mu\nu}=\partial_{\mu}A_{\nu}-\partial_{\nu}A_{\mu}.$ Здесь коэффициент фиксирован. А записывать ли это как $F_{\mu\nu}=\partial_{[\mu}A_{\nu]}$ или как $F_{\mu\nu}=2\partial_{[\mu}A_{\nu]}$ - зависит от того, как определить операцию антисимметризации, здесь единого соглашения нет.

[arseniiv]

Munin в сообщении #1085445 писал(а):

прав в том, что заряд не должен быть единичным, но на его величину попросту надо поделить.

Ну я так и понимал, ибо единичного вообще, как мы знаем, заряда не бывает. Потому мы фиксируем какой-то и он по сравнению с собой становится единичным, потому так и зовём, ну а делить на его величину приходится для получения числа из заряда, являющегося не числом, а элементом одномерного векторного пространства над $\mathbb R$.

[peripatetik]

Munin в сообщении #1085445 писал(а):

arseniiv: прав в том, что "бесконечной малости" в физике не бывает, бывает "пренебрежимая малость".

Не надо путать математический прием с физическим смыслом. В классической механике скорость это производная, хотя что происходит на бесконечно малых расстояниях никому неизвестно.