Т.к. выкладки очень большие и расписывать всё очень долго жаль что нельзя прикреплять документы я бы прикрепил, поэтому
рассказываю что я делал
1. Я перешёл к обобщённой полярной системе

,

2. Посчитал Якобиан он равен

3.Посчитал пределы интегрирования
4.Полученное после перехода к новой системе выражение под корнем внёс под знак дифференциала
посчитал интеграл от 0 до 1
5.Немного преобразовал полученное выражение (домножал на сопряжённые, группировал, сокращал)
6. В итоге у меня получился интеграл
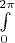

который я не могу посчитать, помогите пожалуйста.
Делал универсальную тригонометрическую подстановку но она ни к чему хорошему не привела, получилось много иррациональности