ItovokiВашу идею пытаются куда-нибудь приспособить в том или ином виде уж лет 500-то точно, но тут есть проблемы.
Допустим, я хочу добавить к полю вещественных чисел

"бесконечно малый элемент"

и "бесконечно большой"
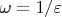
(это ваши АБВ и АМВ). Я хочу, чтобы все числа из полученного расширенного множества можно было умножать и складывать (ведб будет странно, если числа нельзя умножать и складывать).
Как умножить

? Если

, то нарушается известное свойство чисел: нельзя разделить обе части на

, поскольку это дало бы

. Итак, раньше нельзя было делить только на 0, а теперь появился ещё и

, на который тоже нельзя делить: что хорошего?
Во избежание этого кроме

придётся ввести бесконечно малые высшего порядка

,

&c.
Но это не всё: их надо бы складывать. Я не могу положить

. Ведь тогда станет совсем плохо: не только нельзя будет найти решение линеного уравнение

с

как

(ну ладно, пережили бы мы это как-нибудь) - при таком определении от равных отнимаются равные и получаются неравные!
Итак, придётся ввести также

и так далее, а затем и суммы различных бесконечно малых, конечных и бесконечно больших чисел.
На этом пути вас ждёт приятная новость: он приводит к множеству элементов вида

, где

и

вещественные, а равенство и операции определяются как обычно для дробей. Эта конструкция известна, часто применяется и называется
кольцом рациональных функций одной переменной 
.
Но она не снимает проблем: по-прежнему нельзя делить на

(т. е. на настоящий

, а не на

) - ибо раз бесконечно малых много, то неизвестно, какая именно должна получиться (соглашение
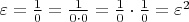
приводит к нарушению хороших свойств чисел и поэтому практически весьма неудобно, как мы видели выше).
Кроме того, здесь сложно определить привычные операции, которые работают с вещественными числами; например, нету "числа"

, которое удовлетворяло бы

- т. е. не существует

.
Желание определить привычные функции для

, пополненного бесконечно большими и бесконечно малыми элементами, приводит к
нестандартному анализу, про который читайте в книжках - но он, как оказывается, является просто переформулировкой обычного анализа и не приводит к принципиально новым результатам.
О различных попытках разрешить трудности, связанные с использованием бесконечно малых, можно почитать в википедии
https://en.wikipedia.org/wiki/Infinitesimal и далее по ссылкам.
Эти мысли ни в коем разе не претендуют на аксиому и т.п. Это мои умозаключения (не мог спокойно спать, пока не поделился ими), которые еще предстоит обработать и в результате или полностью опровергнуть или доработать.
Заранее благодарю за Ваши конструктивные отзывы.
Как видите, ваши мысли не новы: в этом направлении придумали очень много сложных и красивых вещей. Поэтому сперва изучите их - иначе вы навряд ли выдумаете что-то небесполезное. (А перед этим, разумеется, нужно изучить и "обычные" предметы - то есть те, которые рассказывают студентам физикам и математикам на младших курсах.)
Если же не хотите, то просто отставьте ваши размышления, и пусть ломают голову другие.
Вопрос считаю исчерпанным.
Прошу закрыть тему.
Весьма разумно.