Здравствуйте, можете посмотреть, правильно ли я определил сходимость рядов
I ряд:

1)Я рассмотрел ряд из модулей через интегральный признак Коши, интеграл разошелся
2) а)

б) Нашел производную функции:

Она оказалась отрицательной, следовательно из этих трех пунктов ряд условно сходится.
II ряд:
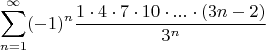
1) Рассмотрел ряд из модулей по признаку Д'Аламбера, предел получился равен

2) а)

б)Так же нашел производную и также она отрицательно, следовательно я сделал вывод что ряд условно сходится.