Быстрота роста ряда производных

[Vitalik2]

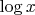
Насколько быстро может расти ряд производных в точке, где функция непрерывна и дифференцируема бесконечное число раз. Ясно, что по модулю не медленнее $n!A^n$ где $n$ - это порядок производной, $A>1$ (для функции $\log x$ в правой полуокрестности точки 0), а может ли расти еще быстрее? Например как $(n!)^2$

[arseniiv]

Не может. Посмотрите на ряд Маклорена такой функции $\sum_{n=0}^\infty n!x^n$. Его слагаемые даже не стремятся к нулю!

[venco]

arseniiv в сообщении #1074624 писал(а):

Не может. Посмотрите на ряд Маклорена такой функции $\sum_{n=0}^\infty n!x^n$. Его слагаемые даже не стремятся к нулю!

А эта функция непрерывна?

[arseniiv]

Ну, ряд расходится не в нуле…

-- Ср ноя 18, 2015 20:38:38 --

Ах да, получается, что я показал, что аналитической такой функции нет, а вот просто непрерывной и бесконечно дифференцируемой — не обязательно. М-да.

[Red_Herring]

известная
Теорема. Для любой последовательности чисел $a_n$ существует б. д. $f$, т.ч. $f^{(n)}(0)=a_n$.

[arseniiv]

(Оффтоп)

Какой учебник анализа мне лучше открывать?

[Otta]

arseniiv
https://www.encyclopediaofmath.org/inde ... on_theorem
https://www.encyclopediaofmath.org/inde ... el_theorem

Вот тут еще хорошо в качестве комментария.