Всем доброго времени суток.
Есть задание: "Решить одномерное нестационарное уравнение (см. формулу ниже) теплопроводности методом сеток."

При граничных условиях:



Область интегрирования

покрываем равномерной сеткой

,

. Для нахождения таблицы решения

воспользуемся следующей конечно разностной схемой:
![$\frac{\overline{u}^{k+1}_i - \overline{u}^k_i}{\tau}=\frac{\omega_r}{h^2} \Bigl[g_{i-1/2}\overline{u}^{k+1}_{i-1} - (g_{i-1/2} + g_{i+1/2}) \overline{u}^{k+1}_i + g_{i+1/2}\overline{u}^{k+1}_{i+1}$ \Bigl] + \\
+ \frac{1 - \omega_r}{h^2} \Bigl[g_{i-1/2}\overline{u}^k_{i-1} - (g_{i-1/2} + g_{i+1/2}) \overline{u}^k_i + g_{i+1/2}\overline{u}^k_{i+1} \Bigl] + \overline{f}_i; \omega_r = 0.5$ $\frac{\overline{u}^{k+1}_i - \overline{u}^k_i}{\tau}=\frac{\omega_r}{h^2} \Bigl[g_{i-1/2}\overline{u}^{k+1}_{i-1} - (g_{i-1/2} + g_{i+1/2}) \overline{u}^{k+1}_i + g_{i+1/2}\overline{u}^{k+1}_{i+1}$ \Bigl] + \\
+ \frac{1 - \omega_r}{h^2} \Bigl[g_{i-1/2}\overline{u}^k_{i-1} - (g_{i-1/2} + g_{i+1/2}) \overline{u}^k_i + g_{i+1/2}\overline{u}^k_{i+1} \Bigl] + \overline{f}_i; \omega_r = 0.5$](https://dxdy-02.korotkov.co.uk/f/5/4/e/54e07d02f9e7b1f8f2ec732b0ce3136682.png)
Граничные условия аппроксимировать следующим образом:

,

Явная схема (

):


Неявная схема (

):


Расчет выполнять до достижения сходимости, т.е. пока

Выдать графики изменения

Тест: при
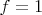
и

точное решение в установившемся режиме

Подберите

и

такими, чтобы выполнялись ваши граничные условия и протестируйте программу для этого случая. Подберите значения

такими, чтобы в установившемся режиме у вас получилось точное решение. После этого подставляйте нужные значения

и

.
Затем идет пример решения для следущих условий:









Пример программы (

или

)
function V1_16_1(N,K,m,wr)
%решение диф ур по неявной схеме
%нестационарное уравнение типа теплопроводности
h=1/N; h2=h^2;
tau=h/2;
q0=0; al0=1; be0=0; q1=0; al1=1; be1=0;
for i=1:N+1
u(i)=0; u1(i)=0; x(i)=(i-1)*h; x1(i)=(i-0.5)*h;
f(i)=1-x(i)^2;
g1(i)=1+x1(i)^2;
end;
t=0;
plot(x,u);
%disp('t='); disp(t);
for kt=1:K
t=t+tau;
for i=2:N
a(i)=wr*tau/h2*g1(i-1);
c(i)=wr*tau/h2*g1(i);
b(i)=-a(i)-c(i)-1;
ad=(1-wr)*tau/h2*g1(i-1);
cd=(1-wr)*tau/h2*g1(i);
bd=-ad-cd+1;
d(i)=-ad*u(i-1)-bd*u(i)-cd*u(i+1)-tau*f(i);
end
c(1)=q0/h; b(1)=al0-q0/h; d(1)=be0;
a(N+1)=-q1/h; b(N+1)=al1+q1/h; d(N+1)=be1; %c(N+1)=0;
%u=mprog(a,b,c,d,N);
ks(1)=-c(1)/b(1);
et(1)=d(1)/b(1);
for i=2:N
z=b(i)+a(i)*ks(i-1);
ks(i)=-c(i)/z;
et(i)=(d(i)-a(i)*et(i-1))/z;
end
u1(N+1)=(d(N+1)-a(N+1)*et(N))/(b(N+1)+a(N+1)*ks(N));
for i=N:-1:1
u1(i)=ks(i)*u1(i+1)+et(i);
end
em=0;
for i=1:N+1
e=abs(u1(i)-u(i));
u(i)=u1(i);
if e>em
em=e;
end
end
if mod(kt,m)==0
hold on
pause(0.1);
plot(x,u);
%t
%disp(u);
end
%if em<0.001
% break
%end
end
hold off
return
Пример программы (

)
function V1_16_0(N,K,m)
%решение диф ур по явной схеме
%нестационарное уравнение типа теплопроводности
h=1/N; h2=h^2;
tau=h2/4;
q0=0; al0=1; be0=0; q1=0; al1=1; be1=0;
for i=1:N+1
u(i)=0; u1(i)=0; x(i)=(i-1)*h; x1(i)=(i-0.5)*h;
f(i)=1-x(i)^2;
g1(i)=1+x1(i)^2;
end;
u(1)=(be0-q0/h*u(2))/(al0-q0/h);
u(N+1)=(be1+q1/h*u(N))/(al1+q1/h);
plot(x,u);
t=0;
%disp('t='); disp(t);
for kt=1:K
t=t+tau;
em=0;
for i=2:N
u1t=u(i)+tau/h^2*(g1(i-1)*u(i-1)-(g1(i-1) + g1(i)) * u(i) + g1(i) * u(i+1)) + tau*f(i);
e=abs(u1t-u1(i));
if e>em;
em=e;
end
u1(i)=u1t;
end
for i=2:N
u(i)=u1(i);
end
u(1)=(be0-q0/h*u(2))/(al0-q0/h);
u(N+1)=(be1+q1/h*u(N))/(al1+q1/h);
if mod(kt ,m)==0
hold on
pause(0.5);
plot(x,u)
disp(u);
% if em<0.001
% break
%end
end
end
hold off
return
Вопрос, собсветнно в чем: помогите, пожалуйста, разобраться что за переменная

, откуда берутся такие значения шага, откуда берутся такие значения векторов

и

. В общем, пожалуйста, прокомментируйте код, в соответсвии с тем, что написано в прилогаемом материале. А то как я не пытался понять почему код написан именно так, у меня не получается.
Заранее спасибо!