Теория чисел, задача о простых числах

[kozlik_kozlik]

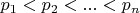
Докажите, что если $p_{1}<p_{2}<...<p_{n}$ - простые числа, то число $p_{1} \cdot p_{2} \cdot ... \cdot p_{n}+1$ либо является простым числом, либо делится на простое число $p>p_{n}$.
Не подскажете, с какого края к этому подходить?

Отвечая на сообщение ниже: ну хорошо, новое число не является одним из $p_{i}$, потому что оно очевидно больше (числа натуральные, их произведение больше или равно любого из них, плюс добавлена единица). Как привести это число в вид, удобный для доказательства?
Ну и ещё оно не делится на любое из этих чисел, потому что прибавлена единица, не делящаяся ни на что, кроме себя, только не знаю, поможет ли это.

[arseniiv]

Сначала покажите, что оно не может быть ни одним из $p_1,\ldots,p_n$. После этого остаток можно будет переформулировать в более удобном для очевидного доказательства виде.

[Deggial]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
Причина переноса: не приведены попытки решения, формулы не оформлены $\TeX$ом

kozlik_kozlik
Приведите попытки решения, укажите конкретные затруднения.
Наберите все формулы и термы $\TeX$ом.
Инструкции по оформлению формул здесь или здесь (или в этом видеоролике).
См. также тему Что такое карантин, и что нужно делать, чтобы там оказаться.
После исправлений сообщите в теме Сообщение в карантине исправлено, и тогда тема будет возвращена.