Два положительных заряда

и

находятся в точках с радиус-векторами

и

. Найти отрицательный заряд

и радиус-вектор

точки, в которую его надо поместить, чтобы сила, действующая на каждый из зарядов была равна нулю.
Понятно, что равновесие возможно, если третий заряд будет находиться на линии, соединяющей два положительных заряда, при чем он будет находиться между этими зарядами.
Расположим заряды 1 и 2 как указано на рисунке
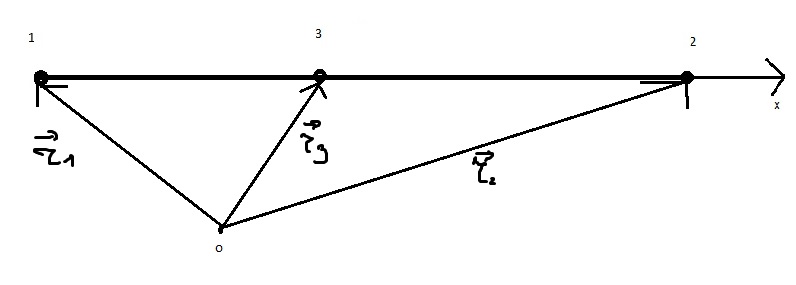
Запишем, например, данное условия для 3 заряда:

А это значит

или

Модули можно убрать, там ведь и так квадраты, поэтому можно выразить


Ошибка где-то закралась. Потому что в ответах вместо минусов плюсы.