Ошибку понял, зря усложнял себе жизнь.
Переписываю функцию:


,

,
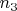
- количество элементов "1", "2" и "3" соответственно. Логарифмирую. Беру производную по

, приравниваю к 0.
Получаю:

А вот теперь вторая часть задания, которую я хотел припрятать, да не вышло. Необходимо проверить, является ли эта оценка эффективной в смысле неравенства Рао-Крамера.
Для эффективной в этом смысле оценки необходимо, чтобы выполнялось равенство:

Где

Нахожу

:

А дальше у меня никак не выходит найти

. Проблем с определениями дисперсии и мат. ожидания не имею, но решительно не понимаю, как связать их с реальными "цифрами". Точнее - не понимаю, как привязать их именно к этому параметру.
Пока что пробую "в лоб", из определений, полученных ещё в ТВ для дискретных величин.
Уточню - затруднение вызывает именно привязка определений мат. ожидания и дисперсии к реалиям МС.
UPD.
Вышеобозначенные действия "в лоб":
Нахожу мат. ожидание распределения, в которое подставляется найденный параметр. Тут же нахожу мат. ожидание квадрата и дисперсию.

И... либо я ткнул мимо, либо неправильно понял условие эффективности по Рао-Крамеру.