Дана окружность с центром в точке

и радиусом

. Точка

делит диаметр

в отношении

, считая от точки

. Через точку

проведена хорда

перпендикулярно диаметру AD . На меньшей дуге AB окружности взята
точка

.
а) Докажите, что

.
б) Найдите площадь четырёхугольника

, если дополнительно известно, что площадь треугольника

равна

.
У меня такая картинка получилась.

По поводу пункта
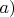
у меня такие соображения. Пусть

. Тогда

, тогда

,

.
Угол

равен тридцати градусам, а значит

, тогда

Далее через площади треугольников пункта
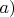
раскрутился (

оказался равносторонним).
По поводу пункта б). Но как его площадь искать? Даже идей нет