Начала статистики, понятие "реализации" случайной величины

[MNikita]

Меня мучает вопрос о том, что такое "реализация случайной величины". Этот оборот появляется, скажем, в определении случайной выборки. Более конкретный пример -- из книги по математической статистике (название указывать не буду, чтобы подчеркнуть вездесущность этого оборота и, одновременно, повсеместное отсутствие объяснения): "Пусть $x_1,x_2,\ldots $ -- координаты точек, взятых наудачу из отрезка $[0,1]$, т.е. независимые и равномерно распределенные на отрезке случайные величины". Ведь здесь тоже речь идет о "реализациях" случайных величин, верно?

Еще, например, в учебниках по статистике приводят определение случайной выборки: "Последовательность наблюдений $X_1,X_2,\ldots X_n$ называется случайной выборкой объема $n$, если $X_i$ получены как независимые реализации некоторой случайной величины $X$ с распределением $F$. При этом говорят, что $X_1,\ldots X_n$ есть выборка из генеральной совокупности $X$".

Разъясните, пожалуйста, что всё это значит. Откуда берутся какие-то случайные величины, и где они определены?

Больше всего меня удручает тот факт, что такой оборот появляется везде, и нигде не объясняется. Заговор?

[ИСН]

Случайная величина - это чёрный ящик. Бьёшь по нему палкой - выскакивает число, каждый раз другое.

[Anton_Peplov]

Случайная величина в результате испытания принимает то или иное значение (в разных испытаниях, вообще говоря, разное). Принятое значение и называется реализацией случайной величины.
Пример: пусть случайная величина - число выпавших очков при броске кости. Выполнено три броска, выпали - при первом броске три очка, при втором - два и при третьем - снова три. Получили три реализации случайной величины - "$3$", "$2$", "$3$".
С ростом числа опытов среднее по всем полученным реализациям будет сходиться по вероятности к математическому ожиданию величины (закон больших чисел).

[arseniiv]

Всё-таки реализация — это случайная величина с таким же законом распределения (совместно независимая со всеми остальными рассматриваемыми реализациями). Иначе сходиться по вероятности нечему будет.

[Anton_Peplov]

arseniiv
Теперь, пожалуйста, еще раз и медленно.

[arseniiv]

Anton_Peplov в сообщении #1006981 писал(а):

С ростом числа опытов среднее по всем полученным реализациям будет сходиться по вероятности к математическому ожиданию величины

Но до этого вы написали, что реализация случайной величины — это какое-то из её значений. Стало быть, несколько реализаций — это кортеж, и кортежи как-то на моей памяти по вероятности ни к чему не сходились. Вот среднее случайных величин $\dfrac{X_1+\ldots+X_n}n$ является случайной величиной $Y_n$, и последовательность таких $Y_n$ уже может куда-то там сходиться по вероятности.

[Anton_Peplov]

Здесь тонкий момент, поэтому давайте попробуем сначала.
Поправьте меня, если я где-то ошибусь в формулировках.
Последовательность случайных величин $\{X_n\}$ называется сходящейся по вероятности к случайной величине $X$, если для любого $\varepsilon > 0$ при $n \to \infty$ верно $P(|X - X_n| < \varepsilon) \to 1$.
Неслучайная величина является частным случаем случайной, поэтому можно рассматривать и $\{X_n\}$, сходящуюся к неслучайному числу.
В результате испытания случайная величина принимает значение (пока не будем пользоваться термином "реализация"). Среднее арифметическое значений случайной величины $X$, полученных в $n$ независимых опытах, само есть случайная величина. Обозначим ее $Y_n$.
Теорема Чебышева (закон больших чисел).
Последовательность $\{Y_n\}$ средних арифметических от значений случайной величины в $n$ независимых опытах сходится по вероятности к ее математическому ожиданию.

Тогда, действительно, моя изначальная фраза не точна (или неверна, как Вам больше нравится).

Вопросы:
1) я правильно сформулировал теорему Чебышева и сопутствующие определения?
2) что же все-таки называется реализацией случайной величины? Я полагаю, что реализацией называется все-таки принятое значение, а фраза, что среднее по реализациям к чему-то там сходится - на моей совести.

[Александрович]

Реализация случайной величины это определение ее значения.

[--mS--]

arseniiv в сообщении #1007009 писал(а):

Всё-таки реализация — это случайная величина с таким же законом распределения (совместно независимая со всеми остальными рассматриваемыми реализациями). Иначе сходиться по вероятности нечему будет.

Это называется "независимыми копиями" (или как-нибудь ещё, но никак не реализациями) данной случайной величины. Последовательность же чисел (значений случайной величины, или реализаций данного набора с.в.) не умеет никуда по вероятности сходиться. Усиленный ЗБЧ утверждает сходимость средних для почти всех реализаций, но не для какой конкретной.

-- Чт апр 23, 2015 08:43:53 --

Опять за дискуссией ТС забыли

MNikita в сообщении #1006965 писал(а):

Меня мучает вопрос о том, что такое "реализация случайной величины". Этот оборот появляется, скажем, в определении случайной выборки. Более конкретный пример -- из книги по математической статистике (название указывать не буду, чтобы подчеркнуть вездесущность этого оборота и, одновременно, повсеместное отсутствие объяснения): "Пусть $x_1,x_2,\ldots $ -- координаты точек, взятых наудачу из отрезка $[0,1]$, т.е. независимые и равномерно распределенные на отрезке случайные величины". Ведь здесь тоже речь идет о "реализациях" случайных величин, верно?

Нет, здесь речь не идёт о реализациях. Реализация возникнет, когда $x_1,x_2,\ldots $ станут числами, полученными в конкретной серии экспериментов.

MNikita в сообщении #1006965 писал(а):

... если $X_i$ получены как независимые реализации некоторой случайной величины $X$ с распределением $F$.

Просто не очень аккуратное словоупотребление. Но если автор не употребляет слова "реализация" в иных смыслах, то здесь это просто более удачный синоним слова "копия".

MNikita в сообщении #1006965 писал(а):

Откуда берутся какие-то случайные величины, и где они определены?

Вы собираетесь бросить точку на отрезок. Потом ещё. И ещё. Результат каждого такого эксперимента в отдельности будет случайной величиной с равномерным распределением. Определённой на $[0,\,1]$ (с соответствующими сигма-алгеброй событий и вероятностью) как $x_i(\omega)=\omega\in[0,\,1]$.
Набор $x_1, x_2, \ldots, x_n$ определён на $n$-мерном кубике $\Omega=[0,\,1]^n$. Этот набор возникает при выборе точки из этого кубика наудачу. Для всякой (заранее взятой, фиксированной, конкретной etc etc) точки $\omega\in [0,\,1]^n$ значение $(x_1(\omega),\ldots,x_n(\omega))=\omega$ будет уже вектором из чисел, т.е. реализацией данной выборки (данного набора случайных величин).

Есть учебники по матстатистике, где слово "реализация" не употребляется ни разу. Боровков, например.

[MNikita]

Благодарю всех за ответы, но я только больше запутался.

ИСН: "Случайная величина - это чёрный ящик. Бьёшь по нему палкой - выскакивает число, каждый раз другое". Не могу не согласиться. Однако в моих примерах речь идет о нескольких случайных величинах. Имеете ли Вы в виду, что у нас есть несколько черных ящиков (и, возможно, несколько палок), а выполняя серию из $n$ экспериментов, мы каждый раз стучим по новому ящику?

--mS--, Вас я совсем не понял. "Вы собираетесь бросить точку на отрезок. Потом ещё. И ещё. Результат каждого такого эксперимента в отдельности будет случайной величиной с равномерным распределением". Хорошо, брошу я одну точку на отрезок. Откуда взяться случайной величине? Вы имеете в виду конкретную: $x_1(\omega)=\omega$...
Насколько я понимаю, вероятностной моделью такого эксперимента -- броска точки -- служит просто отрезок (рассматриваемый как вер. пространство с соответствующей мерой и т.д.).

Можно отвлечься от примера с отрезком (хотя, по видимому, он совершенно типичный), а обратиться к этакой более "прикладной" статистике: изучать, к примеру, зарплаты людей в уездном городе $N$. В таком случае у нас есть случайная величина $\xi$, определенная на множестве жителей: функция, делающая из человека его зарплату. Теперь сделаем выборку объёма $k$: просто случайным образом ткнём пальцем на $k$ понравившихся нам, или не очень, жителей. В $90$% учебников по статистике напишут, что мы располагаем $k$ случайными величинами. Откуда они берутся и как они связаны с $\xi$?

[Александрович]

В последнем примере случайная величина одна - это зарплата.

[Brukvalub]

Итоги:
1. "Реализацией" с.в. называется результат эксперимента, при описании которого на языке математики вознила эта с.в.: например, результат бросания кубика.
2. Понятие "реализация" не дает возможности развивать теорию мат.статистики. Поэтому при получении мат.результатов понятие "реализация" заменяют понятием "копия" с.в. Если сделано много опытов со с.в. и получено много ее "реализаций", то, пытаясь найти закономерность, математик заменяет эти "реализации" на "копии" с.в., рассматривает набор одинаково распределенных независимых с.в. - каждая из этих с.в. соответствует одной из "реализаций".

[_hum_]

--mS-- в сообщении #1007039 писал(а):

Вы собираетесь бросить точку на отрезок. Потом ещё. И ещё. Результат каждого такого эксперимента в отдельности будет случайной величиной с равномерным распределением.

Результат будет числом, являющимся реализацией случайной величины с равномерным распределением.

MNikita, ориентируйтесь на то, что реализация случайной величины - это числовое значение этой случайной величины, полученное в отдельном розыгрыше (эксперименте).

А вообще, удобно представлять себе ситуацию так:

есть исходное (вообще говоря произвольное) множество $\Omega$, с элементами которого "играет Бог", а именно, в каждом эксперименте Бог выбирает какой-то отдельный элемент $\omega$ этого множества, называемый исходом. По какому закону Он это делает, нам неизвестно. Однако известно, что есть закономерность в относительной частоте $\nu$ попадания исхода в некоторые множества $A \subset \Omega$ из так называемой алгебры множеств, или алгебры событий. В общем случае мы можем не видеть непосредственно исходов $\omega$. Зато есть некоторая функция $\xi:\Omega \rightarrow \mathbb{R}$, которая по исходу дает свое значение $x$, которое мы уже реально на практике можем померять. Вот в этой картине функцию $\xi = \xi(\omega)$ и принято относить к понятию случайной величины, а ее значения - к реализациям этой случайной величины.

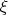
Полезно отметить, что если потом в качестве $\Omega'$ выбрать $\xi(\Omega)$, то на это новое пространство исходов можно перенести всю ту же идеологию. Иными словами, забыть про $\Omega$ и считать, что Бог напрямую играет с числами $x \in \xi(\Omega)$. Тогда обычные числовые функции можно будет рассматривать как случайные величины. Это так называемое индуцированное случайной величиной $\xi $вероятностное пространство.

Все остальное - это не совсем корректное использование этой терминологии (например, "независимые реализации" - это некорректное сокращение для "реализации независимых случайных величин". Ну и т.п.)

[Александрович]

Мне кажется что имеет смысл говорить о реализации события, что случайная величина приняла значение ...

[upgrade]

А принятие величиной $Y$ значения $4$ при принятии величиной $X$ значения $2$ из-за наличия зависимости $Y=2X$ это реализация неслучайной величины?