ВТФ, гиперэллиптические кривые, теорема Фалтингса

[grisania]

Определение 1. Кривая, определяемая уравнением

$y^2=f(x)$,

где $f(x)$ – полином без кратных корней над кольцом целых чисел (коэффициенты целые числа), называется гиперэллиптической.
Род гиперэллиптической кривой.
Определение 2. Степень полинома задаёт род кривой: многочлен степени $2g+1$ или $2g+2$ задаёт кривую рода $g$.
Если степень равна $2g+1$, то кривая называется мнимой гиперэллиптической кривой, а если степень равна $2g+2$, то кривая называется реальной гиперэллиптической кривой.

Переведём кривую Ферма $X^n+Y^n=Z^n$ степени $2g+1$, в гиперэллиптическую кривую рода g. Имеем

$(X^n-Y^n)^2=(X^n+Y^n)^2-4X^nY^n$,
$(X^n-Y^n)^2=Z^{2n}+4(-XY)^n$,
$\left(\frac{X^n-Y^n}{Z^n}\right)^2=4\left(-\frac{XY}{Z^2}\right)^n+1$.

Положив $x=-\frac{XY}{Z^2}$, $y=\frac{X^n-Y^n}{Z^n}$, получаем гиперэллиптическую кривую $y^2=4x^n+1$ рода $g$.
Отметим, что гиперэллиптическая кривая $y^2=4x^{2g+1}+1$ преобразуется в гиперэллиптическую кривую $y^2=x^{2g+1}+4^{2g}$ умножением обеих частей $y^2=4x^{2g+1}+1$ на $4^{2g}$.
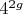
Согласно теореме Фалтингса (Faltings – Fields Medalist) гиперэллиптическая кривая, у которой степень полинома $f(x)$ больше $3$ (род кривой $g>1$), имеет лишь конечное число рациональных точек. Тогда по теореме Фалтингса гиперэллиптическая кривая $y^2=4x^{n}+1$ степени $n=2g+1$, где $g>1$, имеет конечное число рациональных точек, а поэтому кривая Ферма $X^n+Y^n=Z^n$, $n=2g+1$, где $g>1$, имеет конечное число целых точек. Однако, теорема Фалтингса не является эффективный, поскольку не даёт метода вычисления числа рациональных точек на гиперэллиптической кривой. Cohen пишет [2, стр. 369], что методы типа Шаботи (Chabauty-type) могут быть применимы для оценки числа рациональных точек на гиперэллиптической кривой $y^2=4x^{n}+1$ степени $n=2g+1$, где $g>1$. Однако сам Cohen в своём двухтомнике [2,3] этого не делает.

Следовательно, доказательство ВТФ для $n=2g+1$, где $g>1$, сводится к доказательству, что гиперэллиптическая кривая $y^2=4x^{n}+1$ степени $n=2g+1$, где$ g>1$, имеет только две рациональные точки - это $(1,0)$ и $(-1,0)$.

Предположив, что кривая Ферма $X^n+Y^n=Z^n$, $n=2g+1$, $n=2g+1 $ имеет целую точку $(X,Y,Z)$, нетрудно видеть, что гиперэллиптическая кривая будет иметь, кроме рациональных точек $(1,0)$ и $(-1,0)$, ещё шесть рациональных точек – это $\left(\pm\frac{XY}{Z^2}, \frac{X^n-Y^n}{Z^n}\right)$, $\left(\pm\frac{XZ}{Y^2}, \frac{X^n-Z^n}{Y^n}\right)$ и $\left(\pm\frac{ZY}{X^2}, \frac{Z^n-Y^n}{X^n}\right)$.

Если род кривой $g=1$, то гиперэллиптической кривой $y^2=4x^3+1$, очевидно, соответствует эллиптическая кривая $y^2=x^3+16$. Отметим, что если доказывать ВТФ сведением к гиперэллиптическим кривым, то случай $n=3$ является особенным, ибо не выполняется теорема Фалтингса для эллиптической кривой $y^2=x^3+16$.

О теореме Фалтингса и гиперэллиптических кривых можно почитать в [1] и [2,3].

Литература.
1. Степанов С.А. Арифметика алгебраических кривых 1991 http://www.krelib.com/__matematika/1327
2. Cohen H. Number theory vol.1. Tools and diophantine equations (Springer, 2007) http://bookfi.org/book/509928
3. Cohen H. Number theory vol.2. Analytic and modern tools (Springer, 2007) http://bookfi.org/book/509929

[Deggial]

Тема перемещена из форума «Великая теорема Ферма» в форум «Карантин»
Причина переноса: отсутствует предмет обсуждения, формат блога у темы

grisania
Сформулируйте явно предмет обсуждения.
См. также тему Что такое карантин, и что нужно делать, чтобы там оказаться.
После исправлений сообщите в теме Сообщение в карантине исправлено, и тогда тема будет возвращена.