Это фактически означает (независимо от того, что понимается под эм со звёздочкой), что некоторое "элементарное" покрытие множества

имеет меру меньше эпсилона. Но тогда объединение этого покрытия с

будет внешним покрытием

, а разность -- внутренним "покрытием".
По-моему, это ничем не отличается от написанного мной, ну да ладно.
Из фразы в пункте 1, действительно, очевидно, что
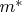
обозначает именно внешнюю меру Жордана (т. е.

мер всех внешних покрытий элементарными множествами).
два определения измеримости по Жордану Лебегу множества

эквивалентны:
1) Инфимум сумм мер всех не более чем счетных внутренних покрытий элементарными множествами равен супремуму сумм мер всех внешних не более чем счетных покрытий.
Существует канторово множество, измеримое по Лебегу и имеющее положительную меру. Очевидно, что любое его элементарное подмножество имеет меру Лебега нуль.