доброго всем времени суток, Уважаемые, помогите c примерчиком, плз.

.
Делаю замену:

при:

и после преобразований получаю:

Делаю еще замену:

, возведу в квадрат и получу:

, подставлю это в (1) и получу:

, откуда:

, т.к.
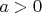
на

, то:

корнем не является. Решая:

по формуле доп.аргумента,

получу:

. Период

отбросил, т.к.

.
Возвращаясь к первой замене, решаю:

и получаю ответ, не совпадающий с ответом задачи:

.
Подскажите, плз, может не правильно решаю?