Проверьте, пожалуйста, правильность хода решения.
Имеется эллипсоид, с малой осью -

. Необходимо доказать, что в общем случае малая ось эллипсоида и нормаль к поверхности эллипсоида не лежат в одной плоскости.
Уравнение эллипсоида:

.
Пусть точка

лежит на поверхности эллипсоида на его малой оси. Точке

соответствует вектор

с координатами

.
Вектор нормали к поверхности эллипсоида

проходит через точку

на поверхности эллипсоида. Точке

соответствует вектор

с координатами

.
Вектор нормали к поверхности эллипсоида

записывается в виде

.
Нахожу смешанное произведение векторов

,

и

:
![$\vec{C} \cdot [\vec{M} \times \vec{N}] = 2\cdot x_0\cdot y_0\cdot c\cdot (\frac{1}{b^2} - \frac{1}{a^2})$ $\vec{C} \cdot [\vec{M} \times \vec{N}] = 2\cdot x_0\cdot y_0\cdot c\cdot (\frac{1}{b^2} - \frac{1}{a^2})$](https://dxdy-04.korotkov.co.uk/f/f/e/e/feea95922405dce062205060d7b5282f82.png)
.
Смешанное произведение в общем случае не рано нулю, поэтому вектора

,

и

не лежат в одной плоскости. Т. е. в общем случае малая ось эллипсоида и нормаль к поверхности эллипсоида не лежат в одной плоскости.
Только в частных случаях
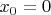
(нормаль лежит в плоскости

) и

(нормаль лежит в плоскости

) смешанное произведение равно нулю.
Для эллипсоида вращения, у которого

смешанное произведение векторов

,

и

равно нулю. Поэтому у эллипсоида вращения нормаль к его поверхности и малая полуось всегда лежат в одной плоскости.
Спасибо.