А откуда мы вообще знаем, что решение сферически симметрично? Это как раз определяется граничными условиями, разве нет?(Мы выбрали, что поле на бесконечности ноль, те потенциал константа)
Вообще говоря, нет. Условие на бесконечности - граничное. А условие симметричности - "пронизывает" всю область, в которой рассматривается уравнение. Ещё частым примером такого "пронизывающего" условия бывает условие стационарности, или колебаний с постоянной заданной частотой - если в уравнения входит время.
Так что, наоборот, граничное условие подчиняется условию сферической симметричности. Невозможно задать сферическую симметричность, и при этом сферически несимметричные гранусловия.
Вообще говоря, можно вообразить себе дифуры, которые при сферически-симметричных гранусловиях имеют не сферически-симметричные решения. Но тогда одна задача будет иметь несколько решений! Не всем это нравится. Если вы работаете в ситуации с существованием и единственностью решения, то сферическая симметричность гранусловий влечёт сферическую симметричность решения.
Пример неединственного решения: волновая функция электрона в атоме водорода (уравнение Шрёдингера, без спина). Задача сферически симметричная, но электрон бывает в разных состояниях, в том числе сферически несимметричных. Это

-орбитали. Они ориентированы в пространстве по-разному, в них электрон крутится вокруг ядра "по кругу", в разные стороны и с разной скоростью. В результате получается целая система решений, которая взятая как единое целое - сферически симметрична.
-- 22.06.2015 19:00:51 --Какое вообще отношение ноль на бесконечности имеет к симметричности?
Ну, он как бы на бесконечности по любому направлению.
(Оффтоп)
(Можно ещё дополнительно рассмотреть ноль на бесконечности отдельно по
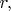
по

и по

...)