Посмотрите, пожалуйста, правильно ли я решаю задачу. Начал с графического способа. Привел к каноническому виду. Сомневаюсь на 5 шаге... переменная входит с коэффициентом -1... а именно

... там ошибка?
где именно в рекомендованной книге изложен симплекс-метод? не могу найти...
Цитата:
Даны условия канонической задачи линейного программирования

Точнее, указаны матрица A и векторы

и

(последний записан строкой). Необходимо последовательно выполнить следующие задания.
1. Применяя вычислительную процедуру симплекс-метода, решить задачу (D,f), т.е. указать ее оптимальный план

и максимальное значение функционала

или установить, что задача

не имеет решения: множество

(пусть) или функционал f не ограничен сверху на

2. Применяя вычислительную процедуру двухфазного симплекс-метода, решить эту же задачу

сравнить результаты и объемы вычислений пп 1 и 2
3. Задачу

решить графически. Сравнить результаты заданий пп 1-3


A

Выпишем математическую модель задачи линейного программирования
Требуется отыскать

при этом на переменные

наложены линейные ограничения
 Решим задачу графически
Решим задачу графически1. Так как переменных 5, а уравнений 3 - графическим методом решать задачу можно
2. Выразим 3 переменные через 2 других

3. Пользуясь условием неотрицательности перейдем к другой системе неравенств

4. Подставим в целевую функцию

и


5. (2) и (3) приведем к каноническому виду
Цитата:
из лекций канонический вид - это
- Все ограничения, кроме условия неотрицательности должны быть со знаком "равно"
- Ограничения, имеющие знак "меньше или равно" можно преобразовать к ограничению со знаком "равно" путем добавления к левой части неотрицательной переменной
- Ограничения, имеющие знак "больше или равно" можно преобразовать к ограничению со знаком "равно" путем вычитания из левой части неотрицательной переменной
- Все свободные члены ограничения должны быть "больше" 0 (если

, то данное ограничение умножаем на -1)
- Все переменные должны быть неотрицательными
-
Если  не подчинено условием неотрицательности, то производим замену
не подчинено условием неотрицательности, то производим замену 



Вопрос в том, что делать со следующим ограничением


вроде как

нужно представить как некую разность ... или все-так можно записать так

Окончательно задача в каноническом виде запишется так

при ограничениях

6. Найдем начальное допустимое базисное решение (НДБР)
Цитата:
из лекций
- сколько л\нез ограничений столько и базисных переменных
- базисные - те переменные, которые встречаются только в одном из ограничений с положительным коэффициентом
- запись НДБР - не базисной переменной присвоить значение 0, а к базисным, значение соответствующих свободных членов


- базисные переменные

- не базисные переменные
Отсюда НДБР
 6. Построим допустимое множество
6. Построим допустимое множество


7. Построим линии уровня

, возьмем


8. Построим график
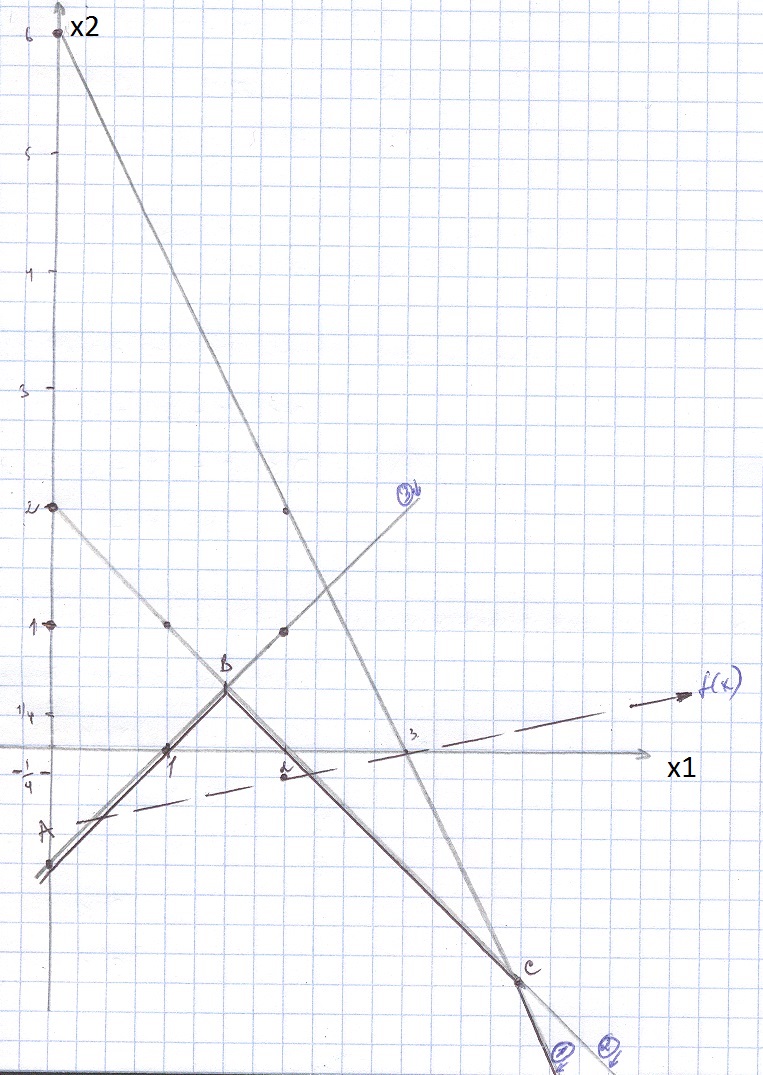
9. Построим grad (т.к. задача на максимум), который показывает направление возрастания или убывания функции
Цитата:
судя по врезке дальше можно записать

я правильно понимаю

только вот не понятно... как по этому градиенту судить о возрастании или убывании функции

10. Определение точек max и min

как это делается? если просто подставить координаты точек пересечения ... то получим 7 в точке А ... но ведь x должны быть "больше или равные 0"? тогда остается только точка B и тут значение функции равно 4... совсем ничего не понимаю :( тут никакого матана применять не надо?
Я думаю,что точкой максимум служит точка B на графике

ответ


Ещё вопрос

на 2 шаге мы выражали 3 переменные через 2... нужно ли переходить назад ко всему набору переменных? ради интереса посмотрел, что исходная функция будет также равна 4 :)