Пусть дано уравнение поверхности

(1), где

(1)
1.
a) Написать систему уравнений, решениями которой являются те и только те тройки числе, являющиеся координатами точек поверхности с уравнением (1), в любой окрестности которых уравнение (1) не определяет

как непрерывную функцию от

и

.
b) Преобразовать систему в равносильную, в которой одно из уравненений есть уравнение цилиндра, с образующими, параллелельными оси

,
c) Выписать уравнение ортогональной проекции на плоскость

множества, обсуждаемого в этом пункте.
2.
а) Найти нижнюю и верхнюю грань значений

на поверхности

.
b) Написать разложение

по формуле Тейлора в каждой точке

, подозрительной на экстремум.
с) Пусть

-- сложная функция, которая получается, если в исследуемую на экстремум функцию подставить

, выраженное из уравнения поверхности, на которой считается экстремум. Не находя явного выражения

написать ее разложение в точке

б соответсвующих точкам

до членов, составляющий второй дифференциал включительно.
d) Сравнить пункты
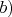
u

и объяснить -- что они дают для решения задачи пункта
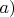
.
Если говорить про 1.Пункт, то я изначально не понимаю -- как начать строить такую систему пункта а). Вроде как

непрерывна везде. Или я не прав?
Во втором пункте как делать пункты а) и b) понимаю очень хорошо, но вот как делать с) и d) не ясно. Выразить

можно легко. Но как не находя явного выражения написать выражение -- не очевидно. Можете подсказать -- в чем тут фишка?