[ Здесь я нахамил. Т.к. тема в карантине, могу только в своём же сообщении исправиться ]
нг писал(а):
Люди! Держите себя в рамках
Извините --- не знаю, отчего меня вчера ночью занесло (т.е. догадываюсь, но это не в тему...)
График функции похож на волнистую (горную) дорогу.
И в каждой точке этой дороги мы чувствуем её наклон --- горизонтальна (

), вниз, слегка вверх (3/100), круто вверх (3/10). Ежели теперь представить себе, что волнистость в какой-то момент (в какой-то точке) прекратилась, дорога стала прямой (не обязательно горизонтальной, а как была с дорожным знаком "наклон 12%", так и осталась, так и ушла в небо) --- это и будет модель касательной к дороге в данной точке. В другой точке касательная --- и к дороге и к графику --- будет другой.
Посмотрите, что ли, для начала на
муки этого парня,
(и здесь), разберитесь с уравнением прямой, проходящей через данную точку с данным наклоном (и похожими задачками --- через две данные точки, например), а потом за касательную принимайтесь... Какая-то там ещё производная возникнет.
Формула у Вас неправильная ---
Цитата:
надо
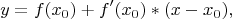

--- это точка, где мы строим касательную,

--- условно говоря, высота этой точки,

--- тот самый наклон в данной точке (3/100, 12%,

),

--- любая точка,

--- расстояние по горизонтали от любой выбранной точки до данной точки

,

или

--- соответствующее смещение по вертикали (подъём, спуск),
![$f(x_0)+[\mbox{это смещение}]$ $f(x_0)+[\mbox{это смещение}]$](https://dxdy-02.korotkov.co.uk/f/d/0/1/d01f0cf77a42be6fb2ec10d9d767be1a82.png)
--- новое значение высоты в любой новой точке

, если, конечно двигаться по прямой-касательной, а не по дороге.