Поигравшись продолжительное время с синтезом фильтров я пришёл к эмпирическому правилу: если один или два полюса являются действительными, а расстояние от нуля на Z-плоскости у остальных комплексно-сопряжённых полюсов меньше или равно этим первым действительным, то импульсная характеристика фильтра получается существенно положительной. Положение нулей при этом особого значения не имеет (в разумных пределах). Это иллюстрируется двумя картинками:
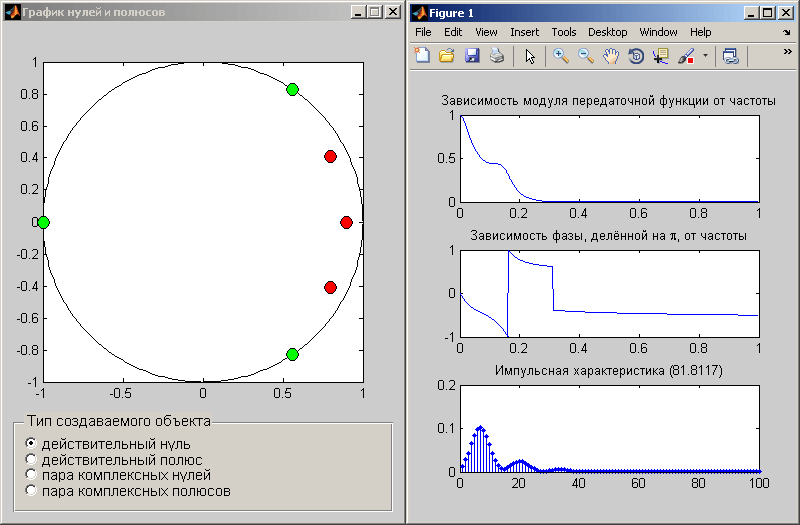
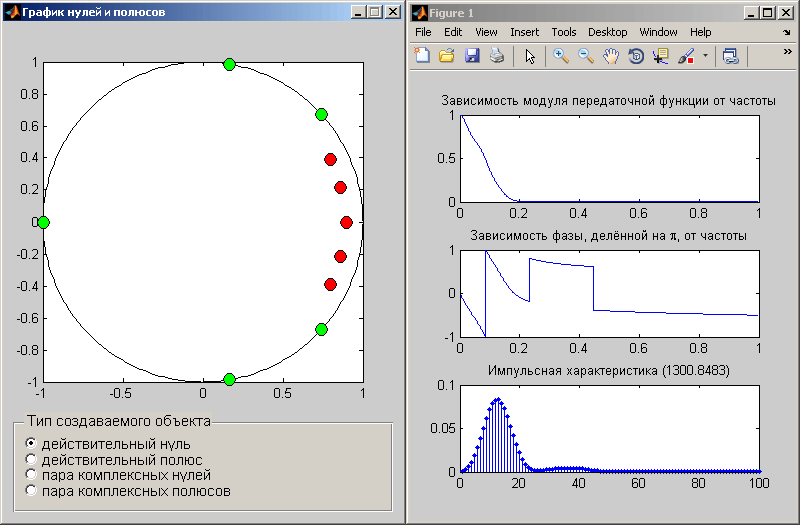
Затем, требование на максимально быстрое затухание в переходной области между полосой пропускания и полосой подавления ФНЧ приводит к тому, что оптимальнее все полюса разместить на нулевой частоте, то есть сделать их действительными. Это эквивалентно последовательному включению нескольких фильтров первого порядка, если бы нули тоже были действительными (как предложил пользователь
levtsn).
Однако, именно нули гораздо оптимальнее расположить не на единичной частоте (то есть не на частоте половины частоты дискритизации), а более-менее равномерно по всей единичной окружности в z-плоскости так, чтобы подавление было максимальным и равномерным во всей полосе подавления. Частота среза по уровню -3 дБ при этом регулируется близостью полюсов к единичной окружности (чем ближе, тем меньше частота среза). Для фильтра 3-го порядка получается что-то такое:
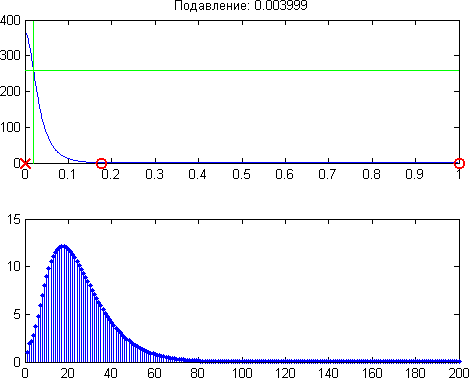
Для синтеза фильтра необходимо задать следующие величины:
— порядок фильтра;
— частоту среза по уровню -3 дБ;
— величину подавления в полосе подавления.
Вне зависимости от этих параметров предлагаемый мною фильтр с положительной импульсной характеристикой будет обладать следующими свойствами:
— все полюса имеют нулевую частоту
— нули расположены по единичной окружности на z-плоскости парами (если порядок нечётный, то один ноль имеет единичную частоту), так, чтобы величина осцилляций в полосе подавления была постоянна.