
ins- писал(а):
Please, take a look at this solution:
…
My goal here is to understand is there some similar "focus"
A trick is a trick exactly for the reason that it is not universal. One can expect that unsing representation of simple fractions he can always solve integral, but he cannot expect that there is a trick giving a nice-looking representation. I think to some degree it might be a fault of education system: students learn tricks without necessary stress that life is tough.
ins- писал(а):
Interesting moment with such integrals is that the denominator cannot be factored in some good looking way and general approach like described here sometimes doesn't work very well.
Actually, you are wrong on both counts. Firstly, the denominator is a polynomial of squares (
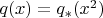
). It means, that with every root
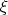
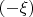
is a root also. So we can group roots and factor



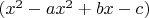
. Although coefficients are complex, factors are quite nice-looking.
Secondly, I have shown above how general approach works, and why one can simplify result of general approach is this particular case.
ins- писал(а):
Such kind of integrals are also a joke with integration software and may be used to show how difficult is to write a good integration software.
I doubt that. They probably used to be, but not any more…
Note on the margin:
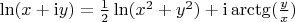
.