qwerlionА в вашем предыдущем посте ошибка вот какая: вы взяли и просто выкинули

, как стремящееся к нулю выражение. А на самом-то деле этого делать нельзя, поскольку вон в той дроби, где синусы да косинусы, если числитель и знаменатель домножить на

и убрать косинус (это можно) останется

, а в общем знаменателе экспоненты -
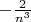
, то есть снова неопределённость

.