--mS--Цитата:
А давайте Вы сформулируете исходную задачу понятнее?
Это формулирование задачи из книги:
Пусть выборка

из

,
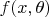
- плотность распределения

в абсолютно непрерывном случае или вероятность

в дискретном случае . Найти эффективную оценку

и параметрическую функцию

, для которой она существует , тремя способами , используя критерий Рао - Крамера , неравенство Рао - Крамера и свойства експоненциальной модели . Неизвестный параметр обозначен через

Я нахожу эффективную оценку и параметрическую функцию. А позже применяю неравенство Рао - Крамера для того чтобы показать , что

является эффективной оценкой параметрической функции

в данной модели
-- 04.05.2015, 20:52 --


\


Цитата:
Ни то, ни другое, ни третье неверно. Найдите распределение

и убедитесь.
Не понимаю