В книге Hinman - "Fundamentals of Mathematical Logic" пишут:
Цитата:
Mathematics is often concerned with theories. Informally a theory involves a collection of results and notions around a common theme. A major concern of Mathematical Logic is the analysis of mathematical theories, and for this purpose we require a more precise specification. A theory will be determined by a particular language and a set T of statements of this language which is closed under logical consequence: if
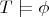
, then already
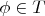
. Then a theory is consistent iff it contains no contradictory statement and complete iff for every statement

of the language, either
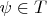
or
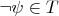
.
Theories arise in two quite different ways: if

is a set of statements, then
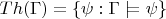
is the theory generated by the members of

considered as axioms, the logical consequences of

;

is called an axiomatic theory; if

is a structure, then
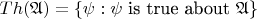
is the theory of the structure. Although the theory of a structure is automatically both consistent and complete, an axiomatic theory may be either, both, or neither.
Не понимаю, почему "theory of a structure is automatically both consistent and complete".
В теории есть только выражения "X истинно для данной структуры", где X - что-то из языка. Значит, для любой структуры мы можем узнать, выполняется ли что-то для неё, если это что-то есть в языке? Если да, почему это считается очевидным?
Что я не так понял?
-- 02.05.2015, 02:09 --Забыл сказать, под структурой подразумевается набор
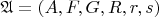
, где

- непустое множество,

и

- функции вида
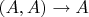
,

- бинарное отношение,

и

- элементы

.
Если в теории есть утвержения вида "

истинно о

", то при вопросах вроде

- множество натуральных чисел, или

- не содержится в образах функций

интуитивно утверждение кажется истинным, но как формализовать, мне непонятно.
Если утверждения вида "в структуре натуральных чисел справедливо

", то даже интуитивно не кажется истинным.