Задача на взвешивание монет.

[mr.tumkan]

Дано $n$ монет, одна из которых фальшивая. Все настоящие монеты весят одинаково, а фальшивая монета отличается по весу от настоящей.
Разрешается сделать а) $3$; б) $k$ взвешиваний на двухчашечных весах без гирь. При каких n при помощи этих взвешиваний можно заведомо определить фальшивую монету и узнать, легче или тяжелее она настоящей?

а) Два взвешивания монет трех монет $a,b,c$ заведомо определят фальшивку (значит три -- тем более).

Если $a=b$, то $c$ -- фальшивка.

Если $a>b$, то нужно еще одно взвешивание. Например, $a$ и $c$. Если $a=c$, то $b$ -- фальшивка. Если $a>c$, то $a$ -- фальшивка. При этом $a<c$ ($b<a<c$) быть не может, так как две монеты имеют один вес.

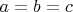
Для четырех монет тоже хватит два взвешивания, так как если в выбранной тройке фальшивка -- мы определим, что она там есть за два взвешивания, если окажется, что $a=b=c$, то ясно, что четвертая фальшивка.

Если пять монет. Берем тройку. Если она покажет два равенства, то берем одну монету $a$ из тройки и $d$. Если равенство, то $e$ фальшивка, если неравенство, то $d$ фальшивка. Если не покажет два равенства, то среди этой тройки фальшивка, какая именно можно одним взвешиванием определить.
То есть для пяти монет хватило три взвешивания.

Для шести монет. Берем две кучки по две монеты. Если равны, то фальшивка из двух оставшихся. Берем из первой четверки одну монету и две оставшиеся. Мы выяснили, что хватит два взвешивания на три монеты, потому в итоге будет три взвешивания.
Если же не было изначально равенства. Значит среди 4 монет -- фальшивка (для этого нужно два взвешивания, как мы выяснили)

Для семи монет берем две кучки по 2 монеты. Если равновесие, то осталась тройка монет, среди которых фальшивка (на это требуется 2 взвешивания еще). Если перевесила одна из кучек, то среди четверки будет фальшивка (на это еще два взвешивания нужно)

Для восьми монет. Берем две кучки по 3 монеты.
Попробуем взять две кучки по 2 монеты. Если равны, то фальшивка в четырех оставшихся, ее можно определить за 2 взвешивания.
Если не будет равновесия, то фальшивка в исходных четырех, что можно определить за 2 взвешивания.

Для девяти монет.
Попробуем взять две кучки по 2 монеты. Если равны, то фальшивка в пяти оставшихся, ее можно определить заведомо еще за 3 взвешивания. То есть такое взвешивание не годится.
Попробуем взять две кучки по 3 монеты. Если будет равновесие, то фальшивка среди трех оставшихся, сможем ее определить за 2 взвешивания. Если одна из кучек перевесит, то фальшивка среди шести, ее можно определить заведомо еще за 3 взвешивания. Такой расклад не годится.
Попробуем две кучки по 4 монеты. Если равновесие, то 9 фальшивка. Если перевесит одна из кучек, то среди восьми фальшивка, но для этого нужно 3 взвешивания. Не годится.
По одной монете взвешивать изначально бессмысленно.
Получается, для девяти монет не хватит трех взвешиваний.
Является ли это достаточным обоснованием?

То есть если монет от 2 до 8, то можно определить фальшивку (и кто тяжелее) за 3 взвешивания, заведомо.

b) Мне кажется, что не случайно $2^3=8$. Наверняка за $k$ взвешиваний можно определить фальшивку в $n\leqslant 2^k$ монет. Можно доказать по индукции, все ясно) База уже проверена, а переход очевиден.

Мне кажется, что у меня слишком долгий пункт а) получился, реально ли это лаконично это описать как-то? Верно ли написано?

[grizzly]

Логика рассуждений хромает. Вы упускаете один очень важный момент -- когда Вы взвешиваете несколько монет, оставляя в стороне остальные, то после неравновесного результата у Вас появляются заведомо эталонные монеты. Научитесь их использовать с большей пользой.
Другие подсказки, я считаю, пока будут слишком преждевременны.

[ИСН]

Написано нормально; чтобы получилось короче, можно выкинуть лишние слова, а доказать очень просто, только там докажется немножко полностью не то, что Вы хотите. Ну, рассмотрим одно взвешивание - сколько у него возможных исходов, например?

[Евгений Машеров]

12 монет проверяются за 3 взвешивания. Это в порядке подсказки.

[mr.tumkan]

ИСН в сообщении #1009920 писал(а):

Написано нормально; чтобы получилось короче, можно выкинуть лишние слова, а доказать очень просто, только там докажется немножко полностью не то, что Вы хотите. Ну, рассмотрим одно взвешивание - сколько у него возможных исходов, например?

Если монеты $a$ и $b$, то $a=b$, $a<b$, $a>b$, то есть три исхода.
Два взвешивания -- 9 исходов. Верно?

[ИСН]

Как-то так. Теперь, а сколько у задачи возможных ответов? Ответ - это типа такого: "Фальшивая монета - вторая, причём она легче".

[mr.tumkan]

ИСН в сообщении #1009940 писал(а):

Как-то так. Теперь, а сколько у задачи возможных ответов? Ответ - это типа такого: "Фальшивая монета - вторая, причём она легче".

Для одного взвешивания ответов 3, для двух взвешиваний 6 (то есть трех монет), для трех взвешиваний 12 (то есть 6 монет). Для $x$ взвешиваний $3\cdot 2^{x-1}$

-- 01.05.2015, 16:29 --

Евгений Машеров в сообщении #1009930 писал(а):

12 монет проверяются за 3 взвешивания. Это в порядке подсказки.

Разве это реально?

[Евгений Машеров]

Да. Есть решение. Не скажу, что просто, там есть одна нетривиальная (даже "антиинтуитивная") догадка касательно сравнений, но работает.

[Shadow]

mr.tumkan в сообщении #1009951 писал(а):

Разве это реально?

Более чем. Если у меня в кармане одна нормальная монета, я и среди 13 найду фальшивую и определю тяжелее она или легче

[ИСН]

mr.tumkan в сообщении #1009951 писал(а):

Для одного взвешивания ответов 3, для двух взвешиваний 6 (то есть трех монет), для трех взвешиваний 12 (то есть 6 монет). Для $x$ взвешиваний $3\cdot 2^{x-1}$

Безотносительно взвешиваний. Никаких нет взвешиваний, 0. Тупо монеты. Ответа мы узнать не можем, но где-то же он есть, правда? Так вот, сколько его вариантов?

[mr.tumkan]

ИСН в сообщении #1010023 писал(а):

mr.tumkan в сообщении #1009951 писал(а):

Для одного взвешивания ответов 3, для двух взвешиваний 6 (то есть трех монет), для трех взвешиваний 12 (то есть 6 монет). Для $x$ взвешиваний $3\cdot 2^{x-1}$

Безотносительно взвешиваний. Никаких нет взвешиваний, 0. Тупо монеты. Ответа мы узнать не можем, но где-то же он есть, правда? Так вот, сколько его вариантов?

Число вариантов в два раза больше числа монет. Верно?

[ИСН]

Выходит, так. Теперь, а как должны быть связаны число исходов и число ответов?

[mr.tumkan]

ИСН в сообщении #1010059 писал(а):

Выходит, так. Теперь, а как должны быть связаны число исходов и число ответов?

Равно, потому как это одно и тоже. Но вот как это увязать с числом взвешиваний, это для меня пока что остается загадкой.

[ИСН]

ИСН в сообщении #1009920 писал(а):

Ну, рассмотрим одно взвешивание - сколько у него возможных исходов, например?

А у двух? А у трёх?

[B@R5uk]

ИСН, вы случайно не клоните к тому, что каждое взвешивание даёт ${{\log }_{2}}3$ бит информации, а всего нам для ответа нужно $1+{{\log }_{2}}N$ бит (где $N$ — число монет)? Тогда, если удастся построить такую последовательность взвешиваний, что каждое новое будет давать новую порцию данных, не повторяющуюся с предыдущими порциями, то ответ становится очевиден. Всегда ли можно такую последовательность построить?