Здравствуйте. Прошу помочь увидеть, что не так в моих рассуждениях, сам просто не вижу, что не так.
В задаче требуется показать, являются ли
и
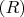
-эффективными оценками дисперсии или нет, если выборка берется из нормального распределения с нулевым средним и дисперсией
. Я показал, что семейство регулярно. Нашел информацию Фишера (в проверке регулярности)
. Вычитал также, что случайная величина
имеет распределение
. Значит, можно просто найти левую часть неравенства Рао - Крамера, а именно - дисперсию.
![$\[\begin{array}{l}
D{S^2} = \frac{{{\sigma ^4}}}{{{n^2}}}D(\frac{{n{S^2}}}{{{\sigma ^2}}}) = \frac{{2{\sigma ^4}(n - 1)}}{{{n^2}}},\\
DS_0^2 = \frac{{{\sigma ^4}}}{{{{(n - 1)}^2}}}D(\frac{{(n - 1)S_0^2}}{{{\sigma ^2}}}) = \frac{{2{\sigma ^4}}}{{n - 1}}
\end{array}\]$](https://dxdy-04.korotkov.co.uk/f/b/7/3/b73696c4f216cad96f87c77701dc1f7082.png "$\[\begin{array}{l}
D{S^2} = \frac{{{\sigma ^4}}}{{{n^2}}}D(\frac{{n{S^2}}}{{{\sigma ^2}}}) = \frac{{2{\sigma ^4}(n - 1)}}{{{n^2}}},\\
DS_0^2 = \frac{{{\sigma ^4}}}{{{{(n - 1)}^2}}}D(\frac{{(n - 1)S_0^2}}{{{\sigma ^2}}}) = \frac{{2{\sigma ^4}}}{{n - 1}}
\end{array}\]$")
. У второй оценки смещение нулевое, а у первой
. Поэтому все теперь можем подставить в неравенство
![$\[D({S^2}) = \frac{{2{\sigma ^4}(n - 1)}}{{{n^2}}} \ge \frac{{{{(1 + {b^'}({\sigma ^2}))}^2}}}{{nI({\sigma ^2})}} = \frac{{2{\sigma ^4}{{(n - 1)}^2}}}{{{n^3}}}\]$](https://dxdy-02.korotkov.co.uk/f/5/4/8/548138dc430ba6756803ef7d4942959982.png "$\[D({S^2}) = \frac{{2{\sigma ^4}(n - 1)}}{{{n^2}}} \ge \frac{{{{(1 + {b^'}({\sigma ^2}))}^2}}}{{nI({\sigma ^2})}} = \frac{{2{\sigma ^4}{{(n - 1)}^2}}}{{{n^3}}}\]$")
. Видно, что равенства нет. Значит, не является
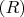
-эффективной, а должна быть. Ну и со второй все тоже понятно, там тоже не выполняется равенство. Вот я в замешательстве, вроде числа все адекватные получаются, а ответ не тот. Что может быть не так?
устремить к бесконечности, то нижняя граница неравенства будет достигнута, это может что-то значить? Например, что она асимптотически эффективная, если так можно говорить вообще.
