В курсе физики Ландау-Лифшица авторы пытаются вывести физические законы нашего мира, основываясь по возможности только на логике, привлекая лишь необходимый минимум экспериментальных фактов. Их подход - это не просто описать наш мир, а показать, что таким он должен быть. В частности в классической механике законы движения получены как следствие принципа наименьшего действия, который вводится как факт. Мне стало интересно можно ли получить законы движения, опираясь исключительно на логику. Постараюсь быть краток.
Замкнутая физическая система со временем меняет свое состояние. Состояние системы в некоторый момент времени должно полностью определяться ее состоянием в предыдущий момент времени, т.к. больше ни чем оно определяться не может. Этот факт отражен в основных уравнениях физики, например уравнение Шредингера. Что бы описать изменение системы математически, системе можно сопоставить некоторую функцию. Вполне возможно введение функции может оказаться недостаточным для полного описания изменения физической системы, возможно для этого потребуется вектор или матрица. Ограничимся пока функцией (S) координат и скоростей объектов системы. Тогда изменение функции S системы, является некоторой функцией функции системы:

Природа не умеет выбирать, следовательно, движение будет только в том направлении, которое не имеет аналогичной альтернативы в смысле значения

. Единственные направления вектора изменения координат

, не имеющие симметричного направления с тем же значением

, это направления вдоль наибольшего и наименьшего изменения функции, т.е. вдоль градиента. Таким образом, система должна развиваться только вдоль градиента функции:

где

- коэффициент пропорциональности. После определения коэффициента

получим «уравнения движения»:

где вектор

описывает совокупное изменение координат:

Время на практике измеряется как координата некоторого независимого циклического процесса. С учетом этого в наше уравнение движения можно ввести время –
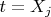
. Уравнение движения примет вид:

До сих пор под

подразумевались координаты и скорости, теперь разделим их

Эти уравнения можно как-то объединить, например

В классической механике принцип наименьшего действия требует, в частности, экстремальность дифференциала действия между двумя бесконечно близкими моментами времени:

т.е. наша функция

это классическое действие и мы должны бы получить те же уравнения Лагранжа. Мне не удалось.
В заключение интересный момент. Если, в результате эволюции системы, градиент в какой-то момент времени становится равным нулю, то изменение действия будет определяться матрицей вторых производных. Можно показать, что в этом случае вектор развития системы совпадает по направлению с собственным вектором матрицы вторых производных, соответствующим экстремальному собственному значению. Тогда уравнением движения будет:

где

удовлетворяет уравнению:
