Нужен совет по оптимизации данного алгоритма.
На вход алгоритм получает

чисел

,

пар

и

пар

.
Далее вычисления выполняются так:
- Случайно, с равномерным законом распределения, выбираем индекс
![$m\in\left[1,N\right]$ $m\in\left[1,N\right]$](https://dxdy-04.korotkov.co.uk/f/f/5/4/f54459da2760c1a1083995986f6ffd4e82.png)
- Вычисляем
 по формуле
по формуле
где
- Вычисляем новое значение
 по формуле
по формуле
- Если еще не все
 обработаны, переходим на п.1;
обработаны, переходим на п.1; - Вывод
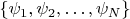
В моей задаче

порядка нескольких тысяч,

, а уложиться надо в несколько миллисекунд на 12-ядерном ксеоне.
Я делаю так: новое значение каждого

вычисляется по формуле

. Видно , что суммы

и

, а также значения

и

можно вычислять заранее, параллельно для всех возможных комбинаций индексов. А после вычисления каждого нового значения

заменять соответствующий ему элемент суммы.
Можно ли еще как-то преобразовать алгоритм, чтобы уменьшить количество вычислений тригонометрических функций ?