Здравствуйте. Такая задача :
Нужно показать асимптотическую нормальность выборочной квантили для истинной квантили.
Что я сделал :
![$\[P(\sqrt n ({X_{([n\delta ] + 1)}} - {F^{ - 1}}(\delta )) < t) = P({X_{([n\delta ] + 1)}} < \frac{t}{{\sqrt n }} + {F^{ - 1}}(\delta ))\]$ $\[P(\sqrt n ({X_{([n\delta ] + 1)}} - {F^{ - 1}}(\delta )) < t) = P({X_{([n\delta ] + 1)}} < \frac{t}{{\sqrt n }} + {F^{ - 1}}(\delta ))\]$](https://dxdy-03.korotkov.co.uk/f/e/a/5/ea568c6923dbbf567404da34d6eb567d82.png)
Дальше вводим новую случайную величину

, которая имеет распределение

. И сумма этих величин есть количество наблюдений
![$\ge [n\delta ] + 1$ $\ge [n\delta ] + 1$](https://dxdy-04.korotkov.co.uk/f/7/7/8/77817241ac09c246564cb0704cff756082.png)
Тогда нашу вероятность можно переписать в виде
![$P({S_n} \ge [n\delta ] + 1)$ $P({S_n} \ge [n\delta ] + 1)$](https://dxdy-02.korotkov.co.uk/f/d/b/a/dba61a7b86a4d6fbe79b767d285943b482.png)
.
Пытаюсь применить ЦПТ. Для этого преобразую к такому виду :
![$$\[P\left(\frac{{{S_n} - E{S_n}}}{{\sqrt {D{S_n}} }} \ge \frac{{[n\delta ] + 1 - nF(\frac{t}{{\sqrt n }} + {F^{ - 1}}(\delta ))}}{{\sqrt {nF(\frac{t}{{\sqrt n }} + {F^{ - 1}}(\delta ))(1 - F(\frac{t}{{\sqrt n }} + {F^{ - 1}}(\delta )))} }}\right)\]$$ $$\[P\left(\frac{{{S_n} - E{S_n}}}{{\sqrt {D{S_n}} }} \ge \frac{{[n\delta ] + 1 - nF(\frac{t}{{\sqrt n }} + {F^{ - 1}}(\delta ))}}{{\sqrt {nF(\frac{t}{{\sqrt n }} + {F^{ - 1}}(\delta ))(1 - F(\frac{t}{{\sqrt n }} + {F^{ - 1}}(\delta )))} }}\right)\]$$](https://dxdy-04.korotkov.co.uk/f/b/f/3/bf3c07632d2e93aca28c00156822142c82.png)
Теперь нужно понять, куда стремится левое слагаемое. Вот все в знаменателе, кроме
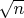
, если очень грубо взять, то к

. А вот с числителем и
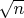
разобраться никак не могу, можно было бы раскрыть по формуле тейлора функцию сверху, но у меня почему-то

получается. Поэтому хотел бы спросить, как мне быть?
Я примерно понимаю, какой ответ получается, но хочется точно знать, почему так.