Исправление опечатки:
До замены переменных при фиксированном
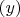
симметричных корней не может быть по теореме Орландо
.
Но Вы неправильную замену сделали.
Shadow, Вы считаете, что правильной заменой для получения симмтричных корней будет, предложенная Вами, т.е.
Было бы истина, если сделали замену

.
.
Я это правильно поняла? (В знаках я, действительно, путаюсь; проверяю на примере и потом забываю, как правильно.) Допустим, что правилен Ваш вариант. Тогда получим уравнение:

.
И никакого противоречия. Но иногда метод срабатывает и удаётся получить противоречие. Гавное, правильно сделать замену переменных. (Об этом я и спрашивала,
Deggial, в недавней теме, но забудем об этом .)
Хочу разместить этот метод для решения некоторого класса диофантовых кубических уравнений третьей степени в дискуссионном разделе или,
Deggial, разумнее это продолжить здесь?