Дифференциальные уравнения

[Smolselena]

1) Доказать что любое решение уравнения $y''+xy=0$ на отрезке $ -25 \leqslant x \leqslant 25$ имеет не менее 15 нулей.
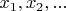
2) Пусть $ x_{1} ,x_{2} ,...$ - расположенные в порядке возрастания последовательные нули решения уравнения $y''+q(x) y=0$,где $ q(x)>0$;при $x_{1} \leqslant x< \infty $функция $q(x)$ непрерывна возрастает.Доказать,что $ x_{n+1}-x_{n}<x_{n}-x_{n-1}$ (т.е. расстояние между соседними нулями убывает)

Подскажите пожалуйста идею решения. У меня только получилось, что если $ m \leqslant q(x) \leqslant M$ и дано 3 уравнения $ z''+m z=0,y''+q(x) y=0,u''+M u=0$, то для расстояния между нулями справедливо неравенство $ \frac{\boldsymbol{\pi}}{ m} \leqslant \boldsymbol{\rho} _{x} \leqslant\frac{\boldsymbol{\pi}}{ M}$

[Brukvalub]

Smolselena в сообщении #994049 писал(а):

...
У меня только получилось, что если $ m \leqslant q(x) \leqslant M$ и дано 3 уравнения $ z''+m z=0,y''+q(x) y=0,u''+M u=0$, то для расстояния между нулями справедливо неравенство $ \frac{\boldsymbol{\pi}}{ m} \leqslant \boldsymbol{\rho} _{x} \leqslant\frac{\boldsymbol{\pi}}{ M}$

Как в этом утверждении используются первое и последнее уравнения?