Интеграл нормального распределения

[llesterr]

Уважаемые гуру в области математики! Взываю к вам о помощи!
Требуется взять интеграл следующего вида:

$\int\limits_{- \infty}^m{\frac{1}{{\sqrt{2\pi}}}\exp (\frac{{-{x^2}}}{2})}\cdot (\frac{1}{2}\cdot (1 + erf(\frac{{n - p \cdot x}}{{\sqrt{2 \cdot (1 -{p^2})}}})))dx$

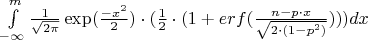
erf - это функция ошибок.
Первый множитель подинтегрального выражения - это функция плотности стандартного нормального распределения;
второй множитель - это уже сама функция распределения.
m, n, p - константы.

Предполагается, что интеграл возможно упростить (через интегрирование по частям и замену переменной) таким образом, чтобы его можно было посчитать через табличные значения (плотности стандартного нормального распределения) и элементарные функции.

По сути этот интеграл является аналогом двойного интеграла плотности нормального стандартного распределения, но выраженный через одномерный интеграл.

Заранее благодарен за помощь!

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- отсутствуют собственные содержательные попытки решения задач(и).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.