Вопрос такой: при каком натуральном

величина

максимальна?
Для краткости обозначим

. Берем производную:

Приравниваем её нулю:



Все отлично, производная слева положительна, справа - отрицательна. Значит, это максимум. Мы получили:
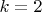
или

Но, что удивительно, если подставить

или

получаются гораздо большие числа! Люди, помогите разобраться