Сторона правильного треугольника

равна

. Треугольник

-- равнобедренный (

). Их плоскости взаимно перпендикулярны. Плоскость
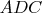
составляет с плоскостью

угол
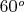
. Найдите площадь треугольника

.
Дело в том, что тут непросто построить линейный угол двугранного угла между плоскостями
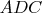
и

. В треугольнике

высота

попадает в середину

(это один перпендикуляр к линии пересечения плоскостей). Вот проблема в том, что в треугольнике
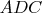
высота

не попадает в середину

(то есть не совпадает с точкой

), а попадает в какую-то левую точку, которую сложно идентифицировать. Как тут быть? Есть ли опечатка? Достаточно ли данных в задаче?