Об альтернативе Фредгольма

[SomePupil]

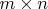
Пусть $A$ - матрица вида $m \times n$ и $\textbf{b}$ вектор в $\mathds{R}^m$. Альтернатива Фредгольма: уравнение $A\textbf{x}= \textbf{b}$ имеет решения тогда и только тогда, когда $\textbf{b} \in \ker(A^T)^\perp$.

Но это же чистой воды фокус! В моей книге (https://www.google.ru/url?sa=t&rct=j&q= ... 1416,d.bGQ) это утверждение дано сразу без какой-либо подготовки.

Форумчане, укажите, пожалуйста, естественное обоснование альтернативы Фредгольма.

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

1) Нарушены правила оформления внешних ссылок (см. Правила форума, п. III.5). В частности, не указана необходимая страница. И пользуйтесь тегами URL.

2) Предмет обсуждения не сформулирован. Да, есть альтернатива Фредгольма. Да, в книге (наверное) тоже что-то написано. Фокус в чем?

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.