ограниченное решение дуфура

[Oleg Zubelevich]

Рассмотрим систему ОДУ

$$\ddot x=f(t,x,\dot x),\quad x=(x^1,\ldots, x^m)\in\mathbb{R}^m\qquad (*)$$

Что бы не перегружать техническими деталями, будем считать, что правая часть системы -- гладкая функция в $\mathbb{R}^{2m+1}$.
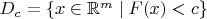
Предположим, что имеется гладкая ( опять-таки что бы не отвлекаться на второстепенное) функция $F:\mathbb{R}^m\to \mathbb{R}$ такая, что при некотором $c$ область $D_c=\{x\in\mathbb{R}^m\mid F(x)<c\}$ гомеоморфна шару пространства $\mathbb{R}^m$ и $\partial D_c=\{x\in\mathbb{R}^m\mid F(x)=c\}$ -- гладкое многообразие ,гомеоморфное сфере.

Докажите следующее утверждение.

Пусть для всех $x\in \partial D_c,\quad t\ge 0$ выполнено неравенство $dF(x)\circ f(t,x,0)>0$. Тогда существует решение $x(t),\quad \dot x(0)=0$ системы (*) такое, что $x(t)\in D_c\quad \forall t\ge 0$.

[Oleg Zubelevich]

задача снимается