Всех приветствую, уважаемые! Столкнулся с такой задачей, которую самостоятельно не могу осилить. Очень долго гуглил прежде чем создать тему. Кое-что нашёл, но не всё.
(Оффтоп)
Можно не читать. К задаче особого отношения не имеет.
---
Задачу ниоткуда не брал, такую не найдёте в учебниках и задачниках (разве что только случайное совпадение). Задачу поставил сам перед собой, сам же её и сформулировал.
Зачем? Очень уж долго рассказывать, но вкратце: делаю игру симулятор, в которой и есть вот такие машины. Зачем учитывать физику в игре и тд? Вот это уж точно долго рассказывать, поэтому примите как есть. Но знайте, это действительно нужно. Хотя бы в упрощённой форме. И нет, меня не устроят разные готовые движки с физикой и тд. Если очень уж интересно зачем это всё, милости прошу в ЛС. Хотя по просьбе могу позже и в теме отписать. Просьба писать только по задаче, а не об игре и реализации. И нет, это не очередные WoT.
Итак!

Машина имеет гусеничный движитель. Масса всей снаряжённой машины
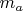
. Радиус ведущего колеса

.
Учитывать силу трения траков о грунт (грунт-сталь). Силу трения в механизмах не учитывать. Какой момент необходимо приложить ведущему колесу, чтобы сдвинуть машину с места с ускорением

под уклоном

?. Одно ведущее колесо слева и одно справа, всего два ведущих колеса. Сопротивление воздуха не учитывать.
---
Пишу своё решение с чего начал.
Руководствовался формулами
отсюда.


- момент статический;

- момент динамический.


- суммарная сила.


Вот тут первый ступор, какую силу трения брать: покоя или качения? Я предполагаю что качения, но
нашёл что нужно брать покоя траков.
Если честно в голове не укладывается как использовать трение покоя в этом случае. А если качения то думаю так:

где

- коэффициент силы трения качения сталь-грунт (кстати, тоже найти не могу).


Что-то мне подсказывает что это не правильно.
Теперь момент динамический.

И вот он самый главный ступор! Не знаю как рассчитать момент инерции всей машины (хотя бы приближённо). Точнее не знаю какую ось взять: проходящая через центр масс или через центр ведущих колёс?
Если взять упрощённо вращающийся прямоугольник, то возможно будет так (вид на машину сверху):


Руководствовался вики.

- ширина машины,

- длина машины.
Теперь ускорение.


---
Ну вот и всё, мои догадки на этом кончились, поэтому прошу помощи в решение задачи.
Заранее благодарю!