Доказательство тождества Паули-Кофинка

[Name XXX]

Недавно я встретил (в одной статье Phys. rev.) доказательство соотношения (Паули-Кофинка)

$$ \bar{\psi}P\gamma_{\mu}\psi Q\gamma^{\mu}\psi = (\bar{\psi}P \psi )Q\psi + \bar{\psi}P\gamma_{5}\psi Q\gamma_{5}\psi . $$

Здесь $Q, P$ являются произвольными матрицами 4*4.

В начале доказательства стартуют с тождеств Паули-Фирца:

$$ \sum_{A}\gamma^{A}_{ab}\gamma^{A}_{cd} = 4\delta_{ad}\delta_{bc}, $$

где $\gamma^{A}$ - одна из 16 базисных матриц пространства спиноров Дирака ($I, \gamma_{\mu}, \gamma_{5}, \frac{1}{2}\gamma_{[\mu}\gamma_{\nu]}, \gamma_{5}\gamma_{\mu}$). Это тождество "вставляется" в $\bar{\psi}P\psi Q \psi$:

$$ \sum_{A}\bar{\psi}P\gamma^{A}\psi P\gamma^{A} \psi = 4\bar{\psi}P\psi Q\psi . $$

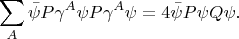
После этого равенство записывается в явном виде

$$ 3\bar{\psi}P\psi Q\psi + \bar{\psi}P\gamma_{\mu}\psi Q\gamma^{\mu}\psi + ... = 4\bar{\psi}P\psi Q\psi . $$

Вопрос: откуда в указанном выражении множитель 3 при слагаемом с $\gamma^{A} = I$?